题目内容
已知:如图,在直角坐标系中,O为原点,点A、B的坐标分别为(3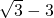 ,0)、(
,0)、( 3+3
3+3 ,0),点C、D在一个反比例函数的图象上,且∠AOC=45°,∠ABC=30°,AB=BC,DA=DB.
,0),点C、D在一个反比例函数的图象上,且∠AOC=45°,∠ABC=30°,AB=BC,DA=DB.
求:点C、D两点的坐标.
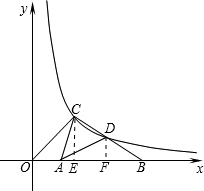 解:过C、D分别作x轴的垂线,垂足分别为E、F,如图,
解:过C、D分别作x轴的垂线,垂足分别为E、F,如图,∵点A、B的坐标分别为(3
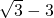 ,0)、(3+3
,0)、(3+3 ,0),
,0),∴AB=3+3
 -(3
-(3 -3)=6,
-3)=6,而∠ABC=30°,AB=BC,
∴BC=AB=6,CE=
 BC=3,
BC=3,又∵∠AOC=45°
∴OE=CE=3,
∴C点坐标为(3,3);
设反比例函数的解析式为y=
 ,
,把C(3,3)代入得k=3×3=9,
∴反比例函数的解析式为y=
 ,
,又∵DA=DB,
∴AF=BF=3,
∴OF=3+3
 -3=3
-3=3 ,
,即点D横坐标为
 ,
,对于y=
 ,令x=3
,令x=3 ,则y=
,则y= =
= ,
,∴D点坐标为(3
 ,
, ).
).分析:过C、D分别作x轴的垂线,垂足分别为E、F,通过A和B的坐标得到AB=6,又∠ABC=30°,AB=BC,根据含30°的直角三角形三边的关系可得CE=
 BC=3,再根据等腰直角三角形的性质得到OE=CE=3,从而确定C点坐标;由C点坐标确定反比例函数的解析式,利用DA=DB,得AF=BF=3,可求得OF=3+3
BC=3,再根据等腰直角三角形的性质得到OE=CE=3,从而确定C点坐标;由C点坐标确定反比例函数的解析式,利用DA=DB,得AF=BF=3,可求得OF=3+3 -3=3
-3=3 ,则令x=3
,则令x=3 ,则y=
,则y= =
= ,得到D点坐标.
,得到D点坐标.点评:本题考查了点在反比例函数图象上,则点的横纵坐标满足其解析式.也考查了等腰三角形的性质以及含30°的直角三角形三边的关系.

练习册系列答案
相关题目

 的图象的一个分支位于第一象限.
的图象的一个分支位于第一象限.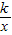 的图象的图象上,求k的值;
的图象的图象上,求k的值; S1?
S1?
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
 中,四边形OABC是矩形,点A,C的坐
中,四边形OABC是矩形,点A,C的坐 =-
=- +
+ 交折线O-A-B于点E.
交折线O-A-B于点E.
