题目内容
(2005•恩施州)如图,AB为圆O的直径,C为圆O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB,延长AB交DC于点E.(1)判定直线DE与圆O的位置关系,并说明你的理由;
(2)求证:AC2=AD•AB;
(3)以下两个问题任选一题作答.(若两个问题都答,则以第一问的解答评分)
①若CF⊥AB于点F,试讨论线段CF、CE和DE三者的数量关系;
②若EC=5
 ,EB=5,求图中阴影部分的面积.
,EB=5,求图中阴影部分的面积.
【答案】分析:(1)DE是⊙O的切线.需连接OC,证明OC⊥DE即可;
(2)证明△DAC∽△CAB即可;
(3)①CF+CE=DE,由角平分线的性质可得,CF=CD,而DC+CE=DE,故CF+CE=DE;
②根据阴影部分的面积=半圆的面积-S△ABC,即可求解.
解答: (1)解:DE是⊙O的切线.(1分)
(1)解:DE是⊙O的切线.(1分)
连接OC,(2分)
∵OA、OC是⊙O的半径,
∴∠OAC=∠OCA.
∵AC是∠DAB的平分线,
∴∠OAC=∠CAD.
∴∠OCA=∠CAD.
∴OC∥AD.
∵AD⊥DE,
∴OC⊥DE.
故DE是⊙O的切线.(4分)
(2)证明:∵AB为⊙O的直径,
∴∠ACB=90°.(5分)
∵AD⊥DE,∠ADC=90°,
∴∠ACB=∠ADC.
∵∠DAC=∠CAB,
∴△DAC∽△CAB.
∴AC2=AD•AB.(7分)
(3)解:①CF+CE=DE.(8分)
∵AC是∠DAB的平分线,且CD⊥AD、CF⊥AF,
∴CF=CD.
∵DC+CE=DE,
∴CF+CE=DE.(10分)
②∵DE是⊙O的切线,
∴∠BCE=∠CAB.
∵∠CEB=∠CEB,
∴△BCE∽△CAE.
∴ .(8分)
.(8分)
∴AE=15,AB=10, ,即CA=
,即CA= BC.
BC.
则在Rt△ABC中,由CA2+BC2=AB2解得:
BC=5,CA=5 .
.
∴S△ABC= .
.
∴阴影部分的面积=半圆的面积-S△ABC= .(10分)
.(10分)
点评:此题综合考查了相似三角形的判定,切线的判定和圆周角定理的综合运用.
(2)证明△DAC∽△CAB即可;
(3)①CF+CE=DE,由角平分线的性质可得,CF=CD,而DC+CE=DE,故CF+CE=DE;
②根据阴影部分的面积=半圆的面积-S△ABC,即可求解.
解答:
 (1)解:DE是⊙O的切线.(1分)
(1)解:DE是⊙O的切线.(1分)连接OC,(2分)
∵OA、OC是⊙O的半径,
∴∠OAC=∠OCA.
∵AC是∠DAB的平分线,
∴∠OAC=∠CAD.
∴∠OCA=∠CAD.
∴OC∥AD.
∵AD⊥DE,
∴OC⊥DE.
故DE是⊙O的切线.(4分)
(2)证明:∵AB为⊙O的直径,
∴∠ACB=90°.(5分)
∵AD⊥DE,∠ADC=90°,
∴∠ACB=∠ADC.
∵∠DAC=∠CAB,
∴△DAC∽△CAB.
∴AC2=AD•AB.(7分)
(3)解:①CF+CE=DE.(8分)
∵AC是∠DAB的平分线,且CD⊥AD、CF⊥AF,
∴CF=CD.
∵DC+CE=DE,
∴CF+CE=DE.(10分)
②∵DE是⊙O的切线,
∴∠BCE=∠CAB.
∵∠CEB=∠CEB,
∴△BCE∽△CAE.
∴
 .(8分)
.(8分)∴AE=15,AB=10,
 ,即CA=
,即CA= BC.
BC.则在Rt△ABC中,由CA2+BC2=AB2解得:
BC=5,CA=5
 .
.∴S△ABC=
 .
.∴阴影部分的面积=半圆的面积-S△ABC=
 .(10分)
.(10分)点评:此题综合考查了相似三角形的判定,切线的判定和圆周角定理的综合运用.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
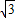 和
和 的⊙O1和⊙O2外切于原点O,在x轴上方的两圆的外公切线AB与⊙O1和⊙O2分别切于点A、B,直线AB交y轴于点C.O2D⊥O1A于点D.
的⊙O1和⊙O2外切于原点O,在x轴上方的两圆的外公切线AB与⊙O1和⊙O2分别切于点A、B,直线AB交y轴于点C.O2D⊥O1A于点D.