题目内容
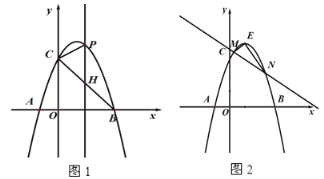
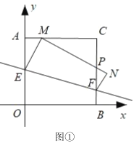
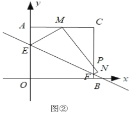
【题目】如图,抛物线![]() 上有一点
上有一点![]() ,
,![]() 的横坐标为1,过
的横坐标为1,过![]() 作
作![]() 轴,与抛物线的另一个交点为
轴,与抛物线的另一个交点为![]() ,且
,且![]() ,作
,作![]() 轴,垂足为
轴,垂足为![]() ,抛物线与
,抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,连结
,连结![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
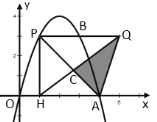
(1)当![]() 时,①求点
时,①求点![]() 的坐标:②求
的坐标:②求![]() 的面积:
的面积:
(2)当![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() 的值.
的值.
【答案】(1)①![]() ;②
;②![]() ;(2)3或
;(2)3或![]()
【解析】
(1)将![]() 代入解析式,先求得P点坐标,再由对称轴求得B点坐标,由
代入解析式,先求得P点坐标,再由对称轴求得B点坐标,由![]() 即可求出Q的坐标;根据图象中的相似三角形可得出
即可求出Q的坐标;根据图象中的相似三角形可得出![]() 的值,由
的值,由![]() 的面积可求得
的面积可求得![]() 的面积;
的面积;
(2)先由解析式得出相关点的坐标,用含b的代数式表示线段的长,当![]() 是以
是以![]() 为腰的等腰三角形时,分两类情况:
为腰的等腰三角形时,分两类情况:![]() 或
或![]() ,分情况求解即可.
,分情况求解即可.
解:(1)①当![]() 时,
时,![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∵![]() 的横坐标为1,
的横坐标为1,
将![]() 代入
代入![]() ,得:
,得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∵![]() 轴,与抛物线的另一个交点为
轴,与抛物线的另一个交点为![]() ,
,![]() ,
,
∴点![]() 与点B关于直线
与点B关于直线![]() 对称,则点
对称,则点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,则
,则![]() ,
,
∴点![]() 的横坐标为 5,
的横坐标为 5,
∴点![]() 的坐标为
的坐标为![]() ;
;
②令![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
∵![]() 轴,
轴,
∴点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 的面积∶
的面积∶![]() 的面积
的面积![]() ,
,
则![]() 的面积∶
的面积∶![]() 的面积
的面积![]() ,
,
∵![]() 的面积
的面积![]() ,
,
∴![]() 的面积
的面积![]() ;
;
(2)由![]() ,得
,得![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() ,
,
∴![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
令![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵![]() 轴
轴
∴![]()
当![]() 是以
是以![]() 为腰的等腰三角形时,则有
为腰的等腰三角形时,则有![]() 或
或![]() ,
,
①当![]() 时,则
时,则![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]()
由![]() 得:
得:![]() ,
,
解得:![]() ;
;
②当![]() 时,
时,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
解得:![]()
综上所述,当![]() 是以
是以![]() 为腰的等腰三角形时,
为腰的等腰三角形时,![]() 的值为3或
的值为3或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c 为常数,且a≠0)的图像上部分点的横坐标x和纵
坐标y的对应值如下表
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … | -3 | -3 | -1 | 3 | 9 | … |
关于x的方程ax2+bx+c=0一个负数解x1满足k<x1<k+1(k为整数),则k=________.