题目内容
如图，已知点E、F在四边形ABCD的对角线延长线上，AE=CF，DE∥BF，∠1=∠2．
（1）求证：
△AED≌△CFB；
（2）若AD⊥CD，四边形ABCD是什么特殊四边形？请说明理由．
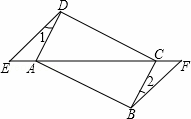
| （1）证明：∵DE∥BF， ∴∠E=∠F， 在△AED和△CFB中，
∴△AED≌△CFB（AAS）； （2）解：四边形ABCD是矩形． 理由如下：∵△AED≌△CFB， ∴AD=BC，∠DAE=∠BCF， ∴∠DAC=∠BCA， ∴AD∥BC， ∴四边形ABCD是平行四边形， 又∵AD⊥CD， ∴四边形ABCD是矩形． |
，
练习册系列答案
名校课堂系列答案
相关题目
计算sin245°+cos30°•tan60°，其结果是（ ）
|
| A． | 2 | B． | 1 | C． |
| D． |
|
的不等式组
的整数解共有5个，则
的取值范围是 。从一栋二层楼的楼顶点A处看对面的教学楼，探测器显示，看到教学楼底部点C处的俯角为45°，看到楼顶部点D处的仰角为60°，已知两栋楼之间的水平距离为6米，则教学楼的高CD是（ ）
|
| A． | （6+6 | B． | （6+3 | C． | （6+2 | D． | 12米 |
）米
）米
的倒数是（ ）
|
| A． | ﹣2 | B． | 2 | C． |
| D． |
|
甲乙两地相距420千米，新修的高速公路开通后，在甲、乙两地行驶的长途客运车平均速度是原来的1.5倍，进而从甲地到乙地的时间缩短了2小时．设原来的平均速度为x千米/时，可列方程为（ ）
|
| A． |
| B． |
| C． |
| D． |
|
+
=2
=2
+
=
+|
﹣1|+（
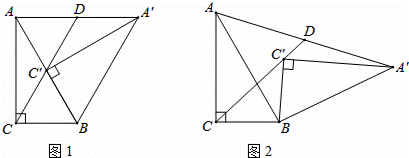
）﹣1﹣2sin45°；