题目内容
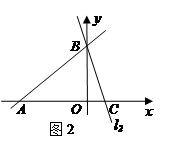
平面直角坐标系中有两点A、B.A的坐标为(1,1),B的坐标为(2,2).若P为x轴上一点,使得PA+PB最短,则P的坐标为________.
( ,0)
,0)
分析:作A关于x轴的对称点A′,连接A′B与x轴相交于一点,根据轴对称-最短路线问题,交点即为所求的点P,设AA′与x轴交点为C,过点B作BD⊥x轴于D,求出△A′CP和△BDP相似,根据相似三角形对应边成比例列式求出 ,然后求出CP的长,再求出OP的长,即可得解.
,然后求出CP的长,再求出OP的长,即可得解.
解答: 解:如图,作A关于x轴的对称点A′,连接A′B与x轴相交于点P,
解:如图,作A关于x轴的对称点A′,连接A′B与x轴相交于点P,
则点P即为使PA+PB最短的点,
设AA′与x轴交点为C,过点B作BD⊥x轴于D,
∵A的坐标为(1,1),B的坐标为(2,2),
∴A′C=1,BD=2,
∵AA′⊥轴,BD⊥x轴,
∴AA′∥BD,
∴△A′CP∽△BDP,
∴ =
= =
= ,
,
∵CD=2-1=1,
∴CP= ×1=
×1= ,
,
∴OP=CO+CP=1+ =
= ,
,
∴点P的坐标为( ,0).
,0).
故答案为:( ,0).
,0).
点评:本题考查了利用轴对称确定最短路线问题,坐标与图形性质,此类题目确定出点P的位置是解题的关键,本题利用相似三角形的判定与性质求出CP与DP的比,再长是解题的关键.
 ,0)
,0)分析:作A关于x轴的对称点A′,连接A′B与x轴相交于一点,根据轴对称-最短路线问题,交点即为所求的点P,设AA′与x轴交点为C,过点B作BD⊥x轴于D,求出△A′CP和△BDP相似,根据相似三角形对应边成比例列式求出
 ,然后求出CP的长,再求出OP的长,即可得解.
,然后求出CP的长,再求出OP的长,即可得解.解答:
 解:如图,作A关于x轴的对称点A′,连接A′B与x轴相交于点P,
解:如图,作A关于x轴的对称点A′,连接A′B与x轴相交于点P,则点P即为使PA+PB最短的点,
设AA′与x轴交点为C,过点B作BD⊥x轴于D,
∵A的坐标为(1,1),B的坐标为(2,2),
∴A′C=1,BD=2,
∵AA′⊥轴,BD⊥x轴,
∴AA′∥BD,
∴△A′CP∽△BDP,
∴
 =
= =
= ,
,∵CD=2-1=1,
∴CP=
 ×1=
×1= ,
,∴OP=CO+CP=1+
 =
= ,
,∴点P的坐标为(
 ,0).
,0).故答案为:(
 ,0).
,0).点评:本题考查了利用轴对称确定最短路线问题,坐标与图形性质,此类题目确定出点P的位置是解题的关键,本题利用相似三角形的判定与性质求出CP与DP的比,再长是解题的关键.

练习册系列答案
相关题目
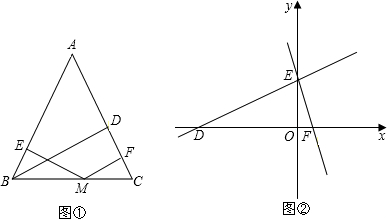

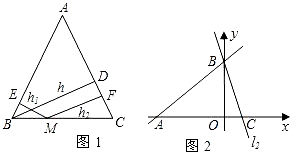
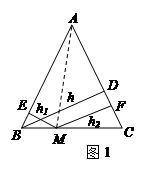
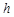 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为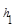 、
、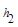 .连接AM,可得结论
.连接AM,可得结论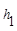 +
+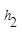 =
=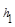 、
、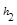 、
、
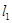 :
: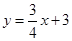 、
、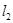 :
: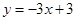 ,若
,若