题目内容
观察两两相交但无三线共点的若干条直线,将平面划分成的区域个数K,有如下事实:一条直线将平面划分成2个区域,K=2=| 1×2 |
| 2 |
| 2×3 |
| 2 |
| 3×4 |
| 2 |
分析:由已知观察各关系式,通过分析总结得出规律,根据规律用n的代表式表示出K.
解答:解:已知一条直线将平面划分成2个区域,K=2=
+1;
两条直线将平面划分成4个区域,K=4=
+1;
三条直线将平面划分成7个区域,K=7=
+1;
则四条直线将平面划分成11个区域,k=11=
+1;
…,
所以n条直线最多可将平面划分成的区域个数K=
+1.
故答案为:
+1.
| 1×2 |
| 2 |
两条直线将平面划分成4个区域,K=4=
| 2×3 |
| 2 |
三条直线将平面划分成7个区域,K=7=
| 3×4 |
| 2 |
则四条直线将平面划分成11个区域,k=11=
| 4×5 |
| 2 |
…,
所以n条直线最多可将平面划分成的区域个数K=
| n(n+1) |
| 2 |
故答案为:
| n(n+1) |
| 2 |
点评:此题考查的是图形数字变化类问题,解题的关键是需要先总结规律,再求解,也是典型题目.

练习册系列答案
相关题目
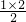 +1;两条直线将平面划分成4个区域,K=4=
+1;两条直线将平面划分成4个区域,K=4=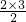 +1;三条直线将平面划分成7个区域,K=7=
+1;三条直线将平面划分成7个区域,K=7=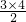 +1;….请根据你的推测,n条直线最多可将平面划分成的区域个数K,用n的代表式表示为K=________.
+1;….请根据你的推测,n条直线最多可将平面划分成的区域个数K,用n的代表式表示为K=________. +1;两条直线将平面划分成4个区域,K=4=
+1;两条直线将平面划分成4个区域,K=4= +1;三条直线将平面划分成7个区域,K=7=
+1;三条直线将平面划分成7个区域,K=7= +1;….请根据你的推测,n条直线最多可将平面划分成的区域个数K,用n的代表式表示为K= .
+1;….请根据你的推测,n条直线最多可将平面划分成的区域个数K,用n的代表式表示为K= .