题目内容
已知关于x的方程x2+px﹣15=0的两根之差的绝对值是8，则P的值是( )
A．±2 B．2 C．﹣2 D．±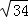
A【考点】根与系数的关系．
【分析】根据根与系数的关系x1•x2=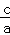
、x1+x2=﹣
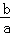得出x1+x2=﹣p，x1•x2=﹣15，再根据（a﹣b）2=（a+b）2﹣4ab代入计算即可．
【解答】解：∵方程x2+px﹣15=0的二次项系数a=1，一次项系数b=p，常数项c=﹣15，
∴x1+x2=﹣p，x1•x2=﹣15，
∵方程x2+px﹣15=0的两根之差的绝对值是8，
∴|x1﹣x2|=8，
∴（x1﹣x2）2=64，
∴（x1+x2）2﹣4x1•x2=64，
∴（﹣p）2﹣4×（﹣15）=64，即p2+60=64，
解得p=±2．
故选A．
【点评】本题主要考查了根与系数的关系．解答此题时，要灵活运用完全平方公式的变形，在该题中就利用了（a﹣b）2=（a+b）2﹣4ab．
练习册系列答案
相关题目
题中假命题是（ ）
x2+bx+c的图象交x轴于A、D两点，并经过B点，已知A点坐标是（2，0），B点的坐标是（8，6）．
B．k≥
可化简为__________．
随
的增大而减小；②图象经过点
．写出
个同时具备条件①、②的一个一次函数表达式 ．
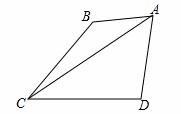如图，四边形ABCD中，AB与CD不平行，AB≠CD，且S△ABC＜S△ACD，过点A画出四边形ABCD的面积等分线，并描述方法．