题目内容
如图，等腰等形ABCD中，AD∥BC，AD=5，∠B=60°，BC=8，且AB∥DE，△DEC的周长是
- A.3
- B.9
- C.15
- D.19
B
分析：由已知可得四边形ABED为平行四边形，即AD=BE从而可求得EC的长，由已知可推出△DEC为等边三角形，从而可求得其周长．
解答：已知等腰梯形ABCD中，AD∥BC，AB∥DE，AD=5，BC=8?BE=5，EC=3
又因为∠B=∠DEC=∠DCE=60°
故△DEC是等边三角形?故周长为9，故选B．
点评：本题考查的是等腰梯形，平行四边形，等边三角形的综合运用．
分析：由已知可得四边形ABED为平行四边形，即AD=BE从而可求得EC的长，由已知可推出△DEC为等边三角形，从而可求得其周长．
解答：已知等腰梯形ABCD中，AD∥BC，AB∥DE，AD=5，BC=8?BE=5，EC=3
又因为∠B=∠DEC=∠DCE=60°
故△DEC是等边三角形?故周长为9，故选B．
点评：本题考查的是等腰梯形，平行四边形，等边三角形的综合运用．
练习册系列答案
相关题目
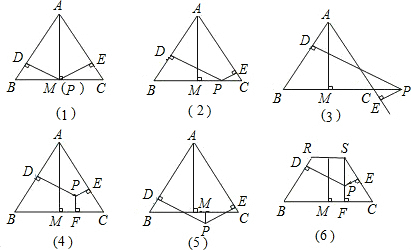
如图是小红设计的钻石形商标，△ABC是边长为2的等边三角形，四边形ACDE是等腰梯形，AC∥ED，∠EAC=60°，AE=1．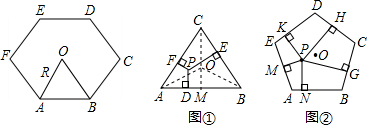
（2012•青岛模拟）同学们已经认识了很多正多边形，现以正六边形为例再介绍与正多边形相关的几个概念．如正六边形ABCDEF各边对称轴的交点O，又称正六边形的中心，其中OA称正六边形的半径，通常用R表示，∠AOB称为中心角，显然．提出问题：正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系？
