Question

【题目】已知，关于x的一元二次方程x2+（1﹣k）x﹣k=0 （其中k为常数）．

（1）判断方程根的情况并说明理由；

（2）若﹣1＜k＜0，设方程的两根分别为m，n（m＜n），求它的两个根m和n；

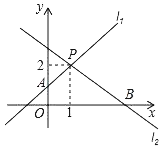
（3）在（2）的条件下，若直线y=kx﹣1与x轴交于点C，x轴上另两点A（m，0）、点B（n，0），试说明是否存在k的值，使这三点中相邻两点之间的距离相等？若存在，求出k的值；若不存在，请说明理由．

Answer 1

【答案】(1) 方程有两个实数根(2) m=k，n=﹣1(3)k=-

【解析】分析：（1）求出判别式的值即可判断．

（2）求出方程的两个根，根据题意即可解决问题．

（3）先求出A、B、C三点坐标，根据题意判断A、B、C的位置，列出方程即可解决问题．

详解：（1）∵△=（1﹣k）2+4k=k2﹣2k+1+4k=k2+2k+1=（k+1）2≥0，∴方程有两个实数根．

（2）∵x2+（1﹣k）x﹣k=0，∴（x﹣k）（x+1）=0，∴x=k或﹣1．

∵﹣1＜k＜0，设方程的两根分别为m，n（m＜n），∴m=k，n=﹣1．

（3）存在．由题意A（k，0），B（﹣1，0），C（，0）．

∵﹣1＜k＜0，∴﹣1＜k＜．

∵AC=AB，∴k﹣=1﹣k，整理得：2k2﹣k+1=0，解得：k=﹣或1（舍弃），

∴当k=﹣时，A、B、C三点中相邻两点之间的距离相等．