题目内容
如图,矩形MNGH的四个顶点都在⊙O上,顺次连接矩形各边的中点,得到菱形ABCD,若BD=12,DF=4,则菱形ABCD的面积为 .
【答案】分析:先连接OH,根据BD=12得出OD长,那么可得到圆的半径为OD+DF,利用三角形全等可得菱形边长等于圆的半径,再根据勾股定理求出OA的长,由S菱形ABCD=4S△AOD即可得出结论.
解答: 解:如图:连接OH,
解:如图:连接OH,
∵BD=12,DF=4
∴⊙O的半径r=OD+DF= BD+DF=
BD+DF= ×12+4=10,
×12+4=10,
∴OH=10
在Rt△HOD与Rt△ADO中,OD=OD,AO=HD,∠AOD=∠HDO=90°
∴△AOD≌△GDO,
∴OH=AD=10,
在Rt△AOD中,
∵AD=10,OD=6,
∴OA= =
= =8,
=8,
∴S菱形ABCD=4S△AOD=4× ×6×8=96.
×6×8=96.
故答案为:96.
点评:本题考查的是菱形的性质及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
解答:
 解:如图:连接OH,
解:如图:连接OH,∵BD=12,DF=4
∴⊙O的半径r=OD+DF=
 BD+DF=
BD+DF= ×12+4=10,
×12+4=10,∴OH=10
在Rt△HOD与Rt△ADO中,OD=OD,AO=HD,∠AOD=∠HDO=90°
∴△AOD≌△GDO,
∴OH=AD=10,
在Rt△AOD中,
∵AD=10,OD=6,
∴OA=
 =
= =8,
=8,∴S菱形ABCD=4S△AOD=4×
 ×6×8=96.
×6×8=96.故答案为:96.
点评:本题考查的是菱形的性质及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

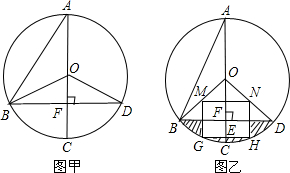
 如图,矩形MNGH的四个顶点都在⊙O上,顺次连接矩形各边的中点,得到菱形ABCD,若BD=12,DF=4,则菱形ABCD的面积为
如图,矩形MNGH的四个顶点都在⊙O上,顺次连接矩形各边的中点,得到菱形ABCD,若BD=12,DF=4,则菱形ABCD的面积为 如图,矩形MNGH的四个顶点都在⊙O上,顺次连接矩形各边的中点,得到菱形ABCD,若BD=12,DF=4,则菱形ABCD的面积为________.
如图,矩形MNGH的四个顶点都在⊙O上,顺次连接矩形各边的中点,得到菱形ABCD,若BD=12,DF=4,则菱形ABCD的面积为________.