题目内容
已知⊙O的半径为 ,弦AB=
,弦AB= ,则AB所对圆周角的度数为 .
,则AB所对圆周角的度数为 .
45°或135°.
【解析】
试题分析:根据题意画出图形,由OC垂直于AB,利用垂径定理得到C为AB的中点,求出AC的长,在直角三角形AOC中,利用勾股定理求出OC=AC,确定出三角形AOC为等腰直角三角形,同理三角形BOC为等腰直角三角形,确定出∠AOB度数,利用圆周角定理即可求出∠ADB与∠AEB的度数.
试题解析:如图所示,
∵OC⊥AB,
∴C为AB的中点,即AC=BC= AB=
AB= ,
,
在Rt△AOC中,OA=r,AC= ,即OC=AC,
,即OC=AC,
根据勾股定理得:OC= ,
,
∴△AOC为等腰直角三角形,
∴∠AOC=45°,
同理∠BOC=45°,
∴∠AOB=∠AOC+∠BOC=90°,
∵∠AOB与∠ADB都对 ,
,
∴∠ADB= ∠AOB=45°,
∠AOB=45°,
∵大角∠AOB=270°,
∴∠AEB=135°,
则弦AB所对的圆周角为45°或135°.
考点:1.圆周角定理;2.垂径定理;3.特殊角的三角函数值.

练习册系列答案
相关题目






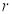 为半径的圆上有且仅有两点到
为半径的圆上有且仅有两点到 轴所在直线的距离等于1,则圆的半径
轴所在直线的距离等于1,则圆的半径 B.
B. C.
C. D.
D.
