题目内容
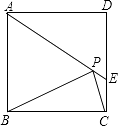
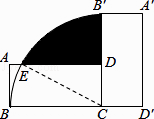
【题目】如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 , 其中正确结论是(填序号)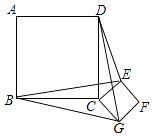
【答案】①②
【解析】解:设BE,DG交于O,
∵四边形ABCD和EFGC都为正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCE+∠DCE=∠ECG+∠DCE=90°+∠DCE,即∠BCE=∠DCG,
在△BCE和△DCG中,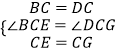 ,
,
∴△BCE≌△DCG(SAS),
∴BE=DG,
∴∠1=∠2,
∵∠1+∠4=∠3+∠1=90°,
∴∠2+∠3=90°,
∴∠BOC=90°,
∴BE⊥DG;故①②正确;
连接BD,EG,如图所示,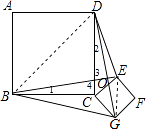
∴DO2+BO2=BD2=BC2+CD2=2a2 , EO2+OG2=EG2=CG2+CE2=2b2 ,
则BG2+DE2=DO2+BO2+EO2+OG2=2a2+2b2 , 故③错误.
所以答案是:①②.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】小明到某超市购买A、B、C三种商品.其中A、B两种商品的单价之和正好等于C商品的单价,小明前两次购买商品的数量和总费用如下表:
商品A的数量 | 商品B的数量 | 商品C的数量 | 总费用(元) | |
第一次 | 2 | 3 | 2 | 230 |
第二次 | 1 | 4 | 3 | 290 |
(1)求A、B、C三种商品的单价;
(2)若小明第三次需要购置A、B、C三种商品共m个,其中C商品的数量是A商品的数量的2倍,恰好花了480元钱.
①求m的最大值;
②若小明在第三次购买A,B,C三种商品时正好遇上“买一送一”活动,即购买一个C商品即可赠送一个A商品或一个B商品(优先赠送A商品),求m的值.