题目内容
抛物线y=-x2-2x+2的开口方向________，顶点坐标为________，对称轴是________．
下 （-1，-3） x=-1
分析：将函数变形为顶点坐标式，再依次判断其各个性质．
解答：∵y=-x2-2x+2=-（x+1）2-3
∴抛物线y=-x2-2x+2的开口方向下，顶点坐标为（-1，-3），对称轴是x=-1．
故答案为：下，（-1，-3），x=-1
点评：本题考查了二次函数的三种形式的转化，二次函数的性质，是基础题，熟练掌握配方法是以及二次函数的性质是解题的关键．
分析：将函数变形为顶点坐标式，再依次判断其各个性质．
解答：∵y=-x2-2x+2=-（x+1）2-3
∴抛物线y=-x2-2x+2的开口方向下，顶点坐标为（-1，-3），对称轴是x=-1．
故答案为：下，（-1，-3），x=-1
点评：本题考查了二次函数的三种形式的转化，二次函数的性质，是基础题，熟练掌握配方法是以及二次函数的性质是解题的关键．
练习册系列答案
相关题目
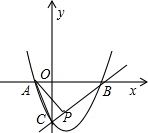A是抛物线与x轴的另一个交点．
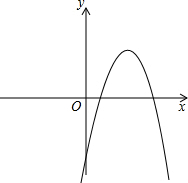已知一元二次方程-x2+bx+c=0的两个实数根是m，4，其中0＜m＜4．
16、已知抛物线y=x2+bx+c的部分图象如图所示，若方程x2+bx+c=0有两个同号的实数根，则c的值可以是