题目内容
已知：a、b、c是△ABC的三边，化简
+
=（ ）
| (a-b+c)2 |
| (a-b-c)2 |
| A、2a-2b | B、2b-2a |
| C、2c | D、-2c |
分析：根据“三角形任意两边之和大于第三边，任意两边之差小于第三边”，得：a-b+c＞0，a-b-c＜0，再根据二次根式的性质进行化简．
解答：解：∵a、b、c是△ABC的三边，
∴a-b+c＞0，a-b-c＜0．
∴原式=a-b+c-a+b+c=2c．
故选C．
∴a-b+c＞0，a-b-c＜0．
∴原式=a-b+c-a+b+c=2c．
故选C．
点评：此题综合考查了三角形的三边关系和二次根式的化简：
=|a|，具有一定的综合性．
| a2 |
练习册系列答案
相关题目
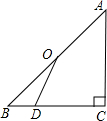已知：如图，点O是等腰直角△ABC斜边AB的中点，D为BC边上任意一点．
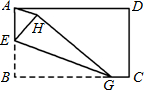12、如图，已知矩形纸片ABCD，点E是AB的中点，点G是BC上的一点，∠BEG＞60°，现沿直线EG将纸片折叠，使点B落在纸片上的点H处，连接AH，则与∠BEG相等的角的个数为