题目内容
 如图,已知∠1=∠2,EF⊥AD于P,交BC延长线于M,求证:∠M=
如图,已知∠1=∠2,EF⊥AD于P,交BC延长线于M,求证:∠M=| 1 |
| 2 |
考点:三角形内角和定理,三角形的外角性质
专题:证明题
分析:由题中条件可得△AEP≌△AFP,∠AEP=∠AFP,而∠AEP=∠B+∠M,∠ACB=∠AFP+∠M,代入即可证.
解答:证明:在△AEP与△AFP中,
∵
,
∴△AEP≌△AFP(ASA),
∴∠AEP=∠AFP(全等三角形的性质),
又∵∠AEP=∠B+∠M①,∠ACB=∠AFP+∠M②,
∴①+②得,2∠M=∠AEP+∠ACB-∠B-∠AFP=∠ACB-∠B,
∴∠M=
(∠ACB-∠B).
∵
|
∴△AEP≌△AFP(ASA),
∴∠AEP=∠AFP(全等三角形的性质),
又∵∠AEP=∠B+∠M①,∠ACB=∠AFP+∠M②,
∴①+②得,2∠M=∠AEP+∠ACB-∠B-∠AFP=∠ACB-∠B,
∴∠M=
| 1 |
| 2 |
点评:本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
两个有理数的和( )
| A、一定大于其中的一个加数 |
| B、一定小于其中的一个加数 |
| C、和的大小由两个加数的符号而定 |
| D、和的大小由两个加数的绝对值而定 |
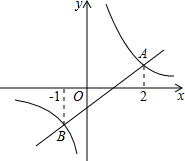 如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=
如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2= 如图,一只蚂蚁从A沿圆柱表面爬到B处,如果圆柱的高为8cm,圆柱的底面半径为
如图,一只蚂蚁从A沿圆柱表面爬到B处,如果圆柱的高为8cm,圆柱的底面半径为