��Ŀ����
����Ŀ����ͼ��,��ƽ��ֱ������ϵ��,ֱ��![]() ��x�ύ��C��,��y�ύ�ڵ�E,��A��x��ĸ�����,��A��ΪԲ��,AOΪ�뾶��Բ��ֱ�ߵ�CE�����ڵ�F,��x�Ḻ��������һ��B.
��x�ύ��C��,��y�ύ�ڵ�E,��A��x��ĸ�����,��A��ΪԲ��,AOΪ�뾶��Բ��ֱ�ߵ�CE�����ڵ�F,��x�Ḻ��������һ��B.
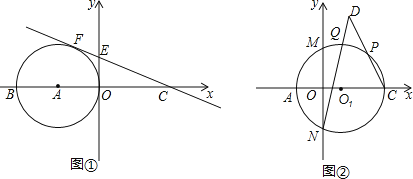
(1)��![]() �İ뾶;
�İ뾶;
(2)��BF��AE,��BF��AE֮����ʲôλ�ù�ϵ?д�����۲�֤��.
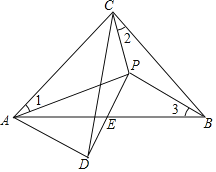
(3)��ͼ��,��ACΪֱ����![]() ��y����M,N����,��P�ǻ�MC������һ��,��Q�ǻ�PM���е�,��CP,NQ,�ӳ�CP,NQ����D��,��CD�ij�.
��y����M,N����,��P�ǻ�MC������һ��,��Q�ǻ�PM���е�,��CP,NQ,�ӳ�CP,NQ����D��,��CD�ij�.
���𰸡�(1)1;(2) BF��AE�������������������3��![]() .
.
��������
��1������AF����ͼ��a����ֱ��EC�Ľ���ʽ�����OE��OC�ij������ݹ��ɶ��������EC�ij���Ȼ��������߳����������EF�ij���Ȼ����Rt��AFC�����ù��ɶ����Ϳ����Բ�İ뾶��
��2������OF����AE�ڵ�H����ͼ��b���������߳������ɵ�EF=EO��EAƽ�֡�FEO�����ݵ��������ε����ʿɵá�AHO=90������BO�ǡ�A��ֱ���ɵá�BFO=90�����Ӷ��õ���BFO=��AHO�����ɵõ�BF��AE��
��3������QC��QM��MC��NC��MO1����ͼ�ڣ���֤��MCQ�ա�DCQ������MC=DC����Rt��MOO1�У����ù��ɶ��������MO�ij���Ȼ����Rt��MOC�У����ù��ɶ����Ϳ����MC�����ɵõ�CD�ij�.
��:(1)����AF,
��ͼ��a.

![]() ֱ��
ֱ��![]() ��x�ύ��C��,��y�ύ��E��,
��x�ύ��C��,��y�ύ��E��,
![]() ��C������Ϊ(2��0),��E������Ϊ��0��
��C������Ϊ(2��0),��E������Ϊ��0��![]() ��,
��,
��OC=2��OE=![]() ��
��
�ߡ�EOC=90����
��EC=![]() ��
��
��AO��OE����ֱ��OE���A�����ڵ�O��
�֡�ֱ��CE���A�����ڵ�F��
���AFC=90����EF=OE=![]() ��
��
��FC=FE+EC=![]()
![]() ��
��
��Rt��AFC��
��AF=����AO=x��AC=x+2��
���ݹ��ɶ����ɵã�x2+��![]()
��2=��x+2��2��
��ã�x=1��
���A�İ뾶Ϊ1��
��2��BF��AE��
֤��������OF����AE�ڵ�H����ͼ��b��

��EF��EO�ֱ����A�����ڵ�F��O��
��EF=EO��EAƽ�֡�FEO��
��EA��OF������AHO=90����
��BO�ǡ�A��ֱ����
���BFO=90����
���BFO=��AHO��
��BF��AE��
��3������QC��QM��MC��NC��MO1����ͼ�ڣ�

��AC�ǡ�O1��ֱ����AC��MN��
��![]() ��
��
���NQC=��MNC��
�ߡ�MQC+��MNC=180������DQC+��NQC=180����
���MQC=��DQC��
�ߵ�Q��![]() ���е㣬
���е㣬
���MCQ=��PCQ��
����MCQ����DCQ��
 ��
��
���MCQ�ա�DCQ��ASA����
��MC=DC��
��OA=1��OC=2��
��AC=3��AO1=![]() ��OO1=f��
��OO1=f��
��Rt��MOO1��
MO1=AO1=![]() ��OO1=
��OO1=![]() ��
��
��![]() ��
��
��Rt��MOC��
MC=![]() ��
��
��DC=![]() ��
��
��CD�ij�Ϊ![]() .
.

 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�