题目内容
 如图,如果∠1=135°,∠2=45°,∠3=100°,那么∠4=________度.
如图,如果∠1=135°,∠2=45°,∠3=100°,那么∠4=________度.
80
分析:根据对顶角相等得到∠5=∠1=135°,则∠5+∠2=135°+45°=180°,根据平行线的判定得到a∥b,再根据平行线的性质有∠3+∠4=180°,然后把∠3=100°代入计算即可.
解答: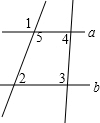 如图,
如图,
∠5=∠1=135°,
而∠2=45°,
∴∠5+∠2=135°+45°=180°,
∴a∥b,
∴∠3+∠4=180°,
∴∠4=180°-∠3=180°-100°=80°.
故答案为80.
点评:本题考查了平行线的判定与性质:同旁内角互补,两直线平行;两直线平行,同旁内角互补.
分析:根据对顶角相等得到∠5=∠1=135°,则∠5+∠2=135°+45°=180°,根据平行线的判定得到a∥b,再根据平行线的性质有∠3+∠4=180°,然后把∠3=100°代入计算即可.
解答:
 如图,
如图,∠5=∠1=135°,
而∠2=45°,
∴∠5+∠2=135°+45°=180°,
∴a∥b,
∴∠3+∠4=180°,
∴∠4=180°-∠3=180°-100°=80°.
故答案为80.
点评:本题考查了平行线的判定与性质:同旁内角互补,两直线平行;两直线平行,同旁内角互补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,如果从半径为9cm的圆形纸片剪去
如图,如果从半径为9cm的圆形纸片剪去| 1 |
| 3 |
| A、6cm | ||
B、3
| ||
| C、8cm | ||
D、5
|
 如图,如果将半径为9cm的圆形纸片剪去一个
如图,如果将半径为9cm的圆形纸片剪去一个| 1 |
| 3 |
| A、6cm | ||
B、3
| ||
C、5
| ||
| D、8cm |
 如图,如果从半径为3cm的圆形纸片剪去
如图,如果从半径为3cm的圆形纸片剪去 如图,如果将半径为9cm的圆形纸片剪去一个
如图,如果将半径为9cm的圆形纸片剪去一个 如图,如果从半径为9cm的圆形纸片剪去
如图,如果从半径为9cm的圆形纸片剪去