题目内容
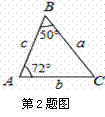
在△ABC中，∠C=∠ABC=2∠A,BD是AC边上的高。求∠DBC. 
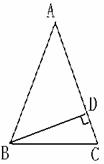
解：设∠A=X°则∠C=∠ABC=2 X°由三角形内角和定理得∠A+∠ABC+∠C=180°
所以有X+2X+2X=180 解得X=36° 所以∠C=72°
因为BD是AC边上的高 所以∠BDC=90所以∠DBC=90°-∠C=90°-72°=18°
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
，宽OC=1， 将△AOC沿AC翻折得△APC.
x2+bx+c上，求b，c的值，并说明点C在此抛物线上；
四边形PnMnNnNn+1的面
积记为Sn，则Sn= 
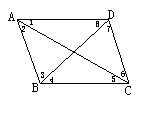C、∠3+∠4+∠5+∠6=1800 D、∠4=∠8
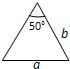
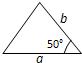
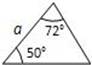
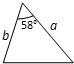如图所示，a,b,c分别表示△ABC的三边长，则下面与△ABC一定全等的三角形是（ ）
