题目内容
在?ABCD中,∠ABC的平分线把AD分成1cm和3cm两部分,则?ABCD的周长等于________cm.
10或14
分析:如图:由?ABCD,根据平行四边形的对边相等且平行,可得AD=BC,AB=CD,AD∥BC,即可得∠AEB=∠CBE,又因为BE是∠ABC的平分线,∴∠ABE=∠CBE,∴∠ABE=∠AEB,∴AB=AE,∠ABC的平分线分对边AD为1cm和3cm两部分,所以AE可能等于1cm或等于3cm,然后即可得出答案.
解答: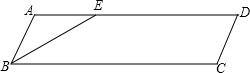 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,AD∥BC,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵∠ABC的平分线分对边AD为1cm和3cm两部分,
如果AE=1cm,则四边形周长为10cm;
如果AE=3cm,则AB=AC=3cm,AD=BC=4cm,
∴?ABCD的周长为14cm;
∴?ABCD的周长为10cm或14cm.
故答案为:10cm或14cm.
点评:此题考查了平行四边形的性质:平行四边形的对边相等且平行.注意当有平行线和角平分线出现时,会有等腰三角形出现.解题时还要注意分类讨论思想的应用.
分析:如图:由?ABCD,根据平行四边形的对边相等且平行,可得AD=BC,AB=CD,AD∥BC,即可得∠AEB=∠CBE,又因为BE是∠ABC的平分线,∴∠ABE=∠CBE,∴∠ABE=∠AEB,∴AB=AE,∠ABC的平分线分对边AD为1cm和3cm两部分,所以AE可能等于1cm或等于3cm,然后即可得出答案.
解答:
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴AD=BC,AB=CD,AD∥BC,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵∠ABC的平分线分对边AD为1cm和3cm两部分,
如果AE=1cm,则四边形周长为10cm;
如果AE=3cm,则AB=AC=3cm,AD=BC=4cm,
∴?ABCD的周长为14cm;
∴?ABCD的周长为10cm或14cm.
故答案为:10cm或14cm.
点评:此题考查了平行四边形的性质:平行四边形的对边相等且平行.注意当有平行线和角平分线出现时,会有等腰三角形出现.解题时还要注意分类讨论思想的应用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
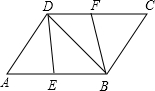 如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD. 如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )
如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )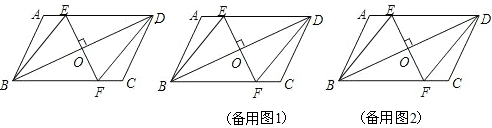
 如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.
如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.