Question

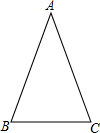
在等腰△ABC中，AB=AC=13，BC=10，取BC所在的直线为x轴，且点B为原点建立直角坐标系．
（1）求△ABC三个顶点的坐标；
（2）求△ABC的面积．

Answer 1

（1）坐标系如图，
过点A作AD⊥BC于D，
∵AB=AC=13，BC=10，
∴BD=CD=

1

2

BC=

1

2

×10=5，
由勾股定理得，AD=

AB2-BD2

=

132-52

=12，
∴A（5，12），B（0，0），C（10，0）；

（2）S_△ABC=

1

2

BC•AD，
=

1

2

×10×12，
=60．