题目内容
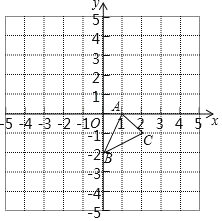
【题目】如图，在平面直角坐标系中，四边形ABCD是平行四边形，OB=OC=2，AB=
.
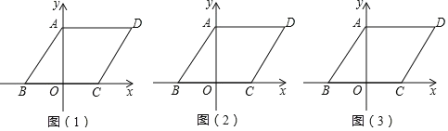
(1)求点D的坐标，直线CD的函数表达式；
(2)已知点P是直线CD上一点，当点P满足S△PAO=
S△ABO时，求点P的坐标；
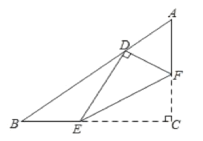
(3)若点M在平面直角坐标系内，则在直线AB上是否存在点F（不与A、B重合），使以A、 C、 F、M为顶点的四边形为菱形?若存在，直接写出F点的坐标，若不存在，请说明理由.
【答案】（1）D（4，3），
；（2）P（3，
）或（-3，
）；（3）F（-3，0）或（2，6）或（
，
）或（
，
）.
【解析】
（1）先求出A点坐标，然后根据菱形的性质得到D点的坐标，利用C，D两点的坐标求出解析式；
（2）利用点P是直线CD上一点，AO为△PAO的底边不变，并且S△PAO=S△ABO，分两种情况讨论即可；
（3）根据菱形的性质，分AC、AF是邻边，AC、AF是邻边，AC是对角线，AF是对角线四种的情况分别进行求解计算．
解：∵OB=OC=2，AB=
，
∴AD=OB+OC=2+2=4，
，
∴A点的坐标为：（0，3），
D点的坐标为：（4，3），
C点的坐标为：（2，0），
设直线CD的函数表达式为：
，
∴将C，D点的坐标代入，得：
，解之得：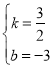
，
∴直线CD的函数表达式为：，
（2）
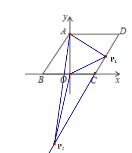
如图示：∵
∴
设P点坐标为（
，
）
即：
，
∴
，
则：
，或
∴
，或
即P点坐标为（
，）或（-3，）；
（3） ∵由（1）得OB=OC=2，AB=，OA=3，
∴AC=，
①当AC、AF是邻边时，如图示，
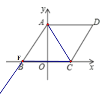
AF=AC=，即点F与B重合，
∴F的坐标为（-3，0），
②当AC、AF是邻边，如图示，
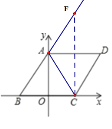
M在直线AD上，且FC垂直平分AM，C，F沿AD成轴对称，
则F的坐标为：（2，6），
③AC是对角线时，如图示：
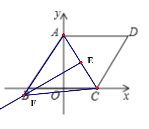
作AC垂直平分线FE，
∵AC经过A（0，3），C（2，0），
∴AC解析式为：
，并且E点的坐标为（1，），
∵
，
∴设FE的解析式为：
，将E点坐标，代入化简得：
FE的解析式为：
又∵AB经过A（0，3），B（-2，0），
∴AB解析式为：
，
∴Ｆ点的坐标为方程组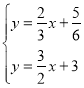
的解，
解之得：
,
∴则F的坐标为：（，）,
④AF是对角线时，如图示：
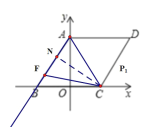
过C作AB垂线，垂足为N，
则
∵
，
∴
，
∴
，
，
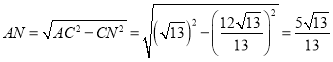设F点的横坐标为
，根据F点在AB上，并AB解析式为：，
∴F的坐标为：（，
）,
则根据勾股定理，有：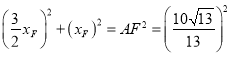
∴
，
，
∴
∴F的坐标为：（，）
综上所述，F点的坐标为：（-3，0）或（2，6）或（，）或（，）
