题目内容
21、如图，要设计一幅长为3xcm，宽为2ycm长方形图案，其中有两横两竖的彩条，横彩条的宽度为acm，竖彩条的宽度bcm，问空白区域的面积是多少？分析：此题可将彩条平移到如图所示的长方形的靠边处，则空白部分组成一个长方形，这个大长方形长（3x-2b）cm，宽为（2y-2a），则空白部分的面积=长×宽即可得出．
解答：
解：可设想将彩条平移到如图所示的长方形的靠边处，将9个小矩形组合成“整体”，
一个大的空白长方形，则该长方形的面积就是空白区域的面积．
而这个大长方形长（3x-2b）cm，宽为（2y-2a）cm．
所以空白区域的面积为（3x-2b）（2y-2a）cm2．
即（6xy-6xa-4by+4ab）cm2．
解：可设想将彩条平移到如图所示的长方形的靠边处，将9个小矩形组合成“整体”，一个大的空白长方形，则该长方形的面积就是空白区域的面积．
而这个大长方形长（3x-2b）cm，宽为（2y-2a）cm．
所以空白区域的面积为（3x-2b）（2y-2a）cm2．
即（6xy-6xa-4by+4ab）cm2．
点评：本题考查了因式分解在实际生活中的应用，题目新颖，要学会用特殊的方法求解．
练习册系列答案
相关题目
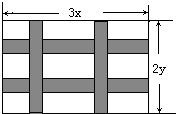如图，要设计一幅长为3xcm，宽为2ycm长方形图案，其中有两横两竖的彩条，横彩条的宽度为acm，竖彩条的宽度bcm，问空白区域的面积是多少？
