题目内容
如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是( )

A.m+n>b+c B.m+n<b+c C.m+n=b+c D.无法确定
A
【解析】
试题分析:延长BA至E点,使得AE=AC,连结ED.EP,可证得△APC≌△APE (SAS),
∴PC=PE=n,△BPE中,PB+PE>AB+AE=AB+AC,即m+n>b+c.
考点:三角形三边关系
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.组成三角形的线段叫做三角形的边.
相邻两边的公共端点叫做三角形的顶点.
相邻两边组成的角叫做三角形的内角,简称三角形的角.
(2)按边的相等关系分类:不等边三角形和等腰三角形(底和腰不等的等腰三角形、底和腰相等的等腰三角形即等边三角形).
(3)三角形的主要线段:角平分线、中线、高.
(4)三角形具有稳定性. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 度数;
度数;


 是二次根式,则
是二次根式,则 应满足的条件是( )
应满足的条件是( ) B.x≥
B.x≥ 墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40
墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40 、-
、- xy、0、m四个式子中有三个是单项式
xy、0、m四个式子中有三个是单项式 是三次二项式
是三次二项式 和6
和6 是同类项
是同类项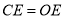 ;③△ODE∽△ADO;④
;③△ODE∽△ADO;④ .其中正确结论有( )
.其中正确结论有( )