一组对边平行且相等.并且对角线互相垂直的四边形是( )A．矩形B．等腰梯形C．正方形D．菱形题目和参考答案——青夏教育精英家教网—

题目内容

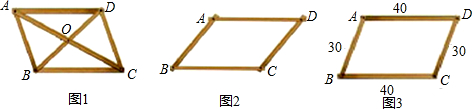
一组对边平行且相等，并且对角线互相垂直的四边形是（　　）

A．矩形

B．等腰梯形

C．正方形

D．菱形

分析：先由一组对边平行且相等的四边形是平行四边形，得出该四边形是平行四边形，再根据对角线互相垂直的平行四边形是菱形判定该四边形是菱形．

解答：解：∵一组对边平行且相等的四边形是平行四边形，
又∵该四边形对角线互相垂直，
∴该四边形是菱形．
故选D．

点评：本题考查了菱形的判定：判定一个四边形是菱形的方法有：①菱形的定义：有一组邻边相等的平行四边形是菱形；②四条边都相等的四边形是菱形；③对角线互相垂直的平行四边形是菱形（或对角线互相垂直平分的四边形是菱形）．

练习册系列答案

A、一组对边相等且有一个角是直角的四边形是矩形

B、一组邻边相等的矩形是正方形

C、一组对边平行且相等的四边形是平行四边形

D、一组邻边相等的平行四边形是菱形

3、下列条件中不能判断四边形是平行四边形的是（　　）

7、下列说法中属于平行四边形判别方法的有（　　）
①两组对边分别平行的四边形是平行四边形 ②平行四边形的对角线互相平分 ③两组对边分别相等的四边形是平行四边形 ④平行四边形的每组对边平行且相等 ⑤两条对角线互相平分的四边形是平行四边形 ⑥一组对边平行且相等的四边形是平行四边形．

（1）小明的爸爸在钉制平行四边形框架时，采用了下面的两种方法．
方法一：如图1，将两根木条AC、BD中点重叠，并用钉子固定，则四边形ABCD就是平行四边形．这样做的依据是：

对角线互相平分的四边形是平行四边形

．
方法二：如图2，将两根同样长的木条AB、CD平行放置，再木条AD、BC加固，则四边形ABCD就是平行四边形．
这样做的依据是：

一组对边平行且相等的四边形是平行四边形

．
方法三：如图3，用两根长40cm的木条AD、BC和两根长30cm的木条AB、CD作为四边形的四条边，并把相等的木条作为相对的边用钉子固定，则四边形ABCD就是平行四边形．这样做的依据是：

两组对边分别相等的四边形是平行四边形

．

（2）2002年世界数学家大会（ICM-2002）在北京召开，这节大会的会标的中央图案是经过艺术处理的“弦图”，它既标志着中国古代的数学成就，又像一只转动的风车，欢迎来自世界各地的数学家们!在这个“弦图”中，隐含着我们学过的一个重要的数学定理，这个定理可以用含a、b、c的等式来表示，它是：

a²+b²=c²

．

试题分类