Question

如图，四边形ABCD为矩形，AB=4，AD=3，动点M从D点出发，以1个单位/秒的速度沿DA向终点A运动，同时动点N从A点出发，以2个单位/秒的速度沿AB向终点B运动、当其中一点到达终点时，运动结束、过点N作NP⊥AB，交AC于点P连接MP、已知动点运动了x秒．
（1）请直接写出PN的长；（用含x的代数式表示）
（2）试求△MPA的面积S与时间x秒的函数关系式，写出自变量x的取值范围，并求出S的最大值；
（3）在这个运动过程中，△MPA能否为一个等腰三角形？若能，求出所有x的对应值；若不能，请说明理由．

Answer 1

解：（1）PN=．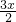

（2）过点P作PQ⊥AD交AD于点Q，
可知PQ=AN=2x
依题意，可得AM=3-x
∴S=•AM•PQ=•（3-x）•2x=-x²+3x
亦即S=-
自变量x的取值范围是：0＜x≤2
∴当x=时，S有最大值，S最大值=

（3）△MPA能成为等腰三角形，共有三种情况：
①当PM=PA时，
∵PQ⊥AD，
∴MQ=AQ=PN=x，
又∵DM+MQ+QA=AD，
∴4x=3，即x=；
②当MP=AM时，由题意：
MQ=AD-AQ-DM=3-，PQ=2x，MP=MA=3-x
在Rt△PMQ中，由勾股定理得：MP²=MQ²+PQ²，
∴（3-x）²=（3-）²+（2x）²
解之得：x=，x=0（不合题意，舍去）
③当AP=AM时，
∵PN∥BC，
∴，
∴AP=，
∵AM=3-x
∴=3-x，
解之得：x=．
综上所述，当x=，或x=，或x=时，△MPA是等腰三角形．
分析：（1）∵NP⊥AB，四边形ABCD为矩形，∴PN∥CB可得；由AB=4，AD=3，可知BC=AD=3；动点动了x秒，可知AN=2x；于是，即PN可求．
（2）△MPA的面积S=AM•AN，AM=AD-DM=3-x，∴S=•（3-x）•2x，动点M由点D到达点A用时间为3秒，动点N由A到B用时间为2秒；N先到达终点，其中一点到达终点时，运动结束，即0＜x≤2．整理S=-，可求S的最大值．
（3）假设△MPA为一个等腰三角形，则会有PM=PA或MP=AM或AP=AM．
过点P作PQ⊥AD交AD于点Q
①当PM=PA时，据PQ⊥AD，得MQ=QA=PN=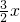，又DM+MQ+QA=AD，所以4x=3，即x可求．
②当MP=AM时，由题意：MQ=AD-AQ-DM=3-，PQ=2x，MP=MA=3-x，在Rt△PMQ中，由勾股定理得：MP²=MQ²+PQ²，x可求．
③当AP=AM时，由PN∥BC，得，于是AP=，又AM=3-x，则=3-x，即x可求．综合可知△MPA能为一个等腰三角形．
点评：此题为综合应用类型的题目，有难度，但能考查综合知识点运用的能力．