题目内容
【题目】已知x2=1,求![]() 的值.
的值.
解:因为![]() ,所以
,所以![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]() 无意义
无意义
所以![]() 的值是1
的值是1
(1)错因:_________________________________.
(2)纠错: _________________________________.
【答案】错在认为负数没有立方根,漏掉了当x=-1时,![]() =-1, 因为x2=1,所以x=±1.当x=1时,
=-1, 因为x2=1,所以x=±1.当x=1时,![]() =
=![]() =1;当x=-1时,
=1;当x=-1时,![]() =
=![]() =-1,所以
=-1,所以![]() 的值是1或-1.
的值是1或-1.
【解析】
如果一个数x的立方等于a,那么x是a的立方根,根据此定义求解即可.
解:(1) 此题错在认为负数没有立方根,漏掉了当x=-1时,![]() =-1;
=-1;
(2) 因为x2=1,所以x=±1.
当x=1时,![]() =
=![]() =1;
=1;
当x=-1时,![]() =
=![]() =-1,
=-1,
所以![]() 的值是1或-1.
的值是1或-1.
故答案为: (1). 错在认为负数没有立方根,漏掉了当x=-1时,![]() =-1, (2). 因为x2=1,所以x=±1.当x=1时,
=-1, (2). 因为x2=1,所以x=±1.当x=1时,![]() =
=![]() =1;当x=-1时,
=1;当x=-1时,![]() =
=![]() =-1,所以
=-1,所以![]() 的值是1或-1.
的值是1或-1.

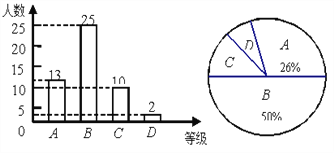
【题目】为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为![]() (分),且
(分),且![]() ,将其按分数段分为五组,绘制出以下不完整表格:
,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩 | 频数(人数) | 频率 |
一 |
| 2 | 0.04 |
二 |
| 10 | 0.2 |
三 |
| 14 | b |
四 |
| a | 0.32 |
五 |
| 8 | 0.16 |
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有 名学生参加;
(2)直接写出表中a= ,b= ;
(3)请补全下面相应的频数分布直方图;

(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 。
【题目】(1)填表:
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你发现了什么规律?请用语言叙述这个规律:______________________________.
(3)根据你发现的规律填空:
①已知![]() =1.442,则
=1.442,则![]() =__________,
=__________,![]() =__________;
=__________;
②已知![]() =0.076 96,则
=0.076 96,则![]() =__________.
=__________.