题目内容
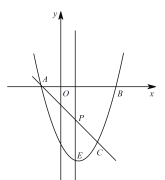
【题目】如图,一次函数y=![]() x+3的图象分别与y轴,x轴交于点A,B,点P从点B出发,沿射线BA以每秒1个单位的速度运动,设点P的运动时间为t秒.
x+3的图象分别与y轴,x轴交于点A,B,点P从点B出发,沿射线BA以每秒1个单位的速度运动,设点P的运动时间为t秒.

(1)点P在运动过程中,若某一时刻,△OPA的面积为3,求此时P的坐标;
(2)在整个运动过程中,当t为何值时,△AOP为等腰三角形?请直接写出t的值.
【答案】(1)点P的坐标为(﹣2,![]() )或(2,
)或(2,![]() );(2)当t的值为2、8、
);(2)当t的值为2、8、![]() 和
和![]() 时,△AOP为等腰三角形.
时,△AOP为等腰三角形.
【解析】
(1)根据坐标轴上点的坐标特征可求得A、B的坐标,用m表示出点P的坐标,利用面积可求得m的值,进一步求得P点坐标;
(2)可用t表示出BP、AP的长,分AP=AO、AP=OP和OP=AO三种情况,分别得到关于t的方程,可求得t的值.
(1)当x=0时,y=3,
当y=0时,x=4,
则A(0,3),B(4,0),
∴AO=3,BO=4,
设点P的坐标为(m,![]() m+3),
m+3),
∵△OPA的面积为3,
∴![]() ×3×|m|=3,
×3×|m|=3,
解得:m=±2,
∴点P的坐标为(﹣2,![]() )或(2,
)或(2,![]() ).
).
(2)∵AO=3,BO=4,
∴AB=![]() ,
,
由题意可知BP=t,AP=5﹣t,
当△AOP为等腰三角形时,有AP=AO、AP=OP和AO=OP三种情况.
①当AP=AO时,则有5﹣t=3,解得t=2;或t﹣5=3,解得t=8;
②当AP=OP时,过P作PM⊥AO,垂足为M,如图1,

则M为AO中点,故P为AB中点,此时t=![]() ;
;
③当AO=OP时,过O作ON⊥AB,垂足为N,过P作PH⊥OB,垂足为H,如图2,

则NP=AN=![]() AP=
AP=![]() (5﹣t),
(5﹣t),
∵S△AOB=![]() ,
,
∴ON=![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴t=![]() ,
,
综上可知当t的值为2、8、![]() 和
和![]() 时,△AOP为等腰三角形.
时,△AOP为等腰三角形.

 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】某公司欲将![]() 件产品全部运往甲,乙,丙三地销售(每地均有产品销售),运费分别为40元/件,24元/件,7元/件,且要求运往乙地的件数是运往甲地件数的3倍,设安排
件产品全部运往甲,乙,丙三地销售(每地均有产品销售),运费分别为40元/件,24元/件,7元/件,且要求运往乙地的件数是运往甲地件数的3倍,设安排![]() (
(![]() 为正整数)件产品运往甲地.
为正整数)件产品运往甲地.
(1)根据信息填表:
甲地 | 乙地 | 丙地 | |
产品件数(件) |
|
| |
运费(元) |
|
(2)若总运费为6300元,求![]() 与
与![]() 的函数关系式并求出
的函数关系式并求出![]() 的最小值.
的最小值.