题目内容
如图,点D在反比例函数y=| k |
| x |
(1)求反比例函数的解析式;

(2)点B为横坐标为1的反比例函数图象上的一点,BA、BE分别垂直x轴和y轴,连接OB,将OABE沿OB折叠,使A点落在点A′处,A′B与y轴交于点F,求OF的长;

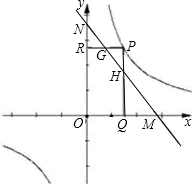
(3)直线y=-x+3交x轴于M点,交y轴于N点,点P是双曲线y=
| k |
| x |
分析:(1)由于三角形OCD是等腰直角三角形,不难得出D(2,2),将其代入反比例函数的解析式y=
(k>0)中即可求出k的值;
(2)根据折叠的性质不难得出△EBF≌△A'OF,那么A′F=OE-OF,可先求出B点坐标,即可得出OE,OA′的长,如果设OF=x,那么A′F=OE-x,可在直角三角形A′OF中,用勾股定理求出x即OF的长;
(3)根据直线MN的解析式可知:三角形MON是等腰直角三角形,那么∠NMO=45°,如果过G作x轴的垂线,不难得出MG=
OP,同理可得出NH=
PR,因此MG•NH=2OP•PR,而OP•PR=k(k的值在(1)题已经求出),因此MG•NH的值是不变的.
| k |
| x |
(2)根据折叠的性质不难得出△EBF≌△A'OF,那么A′F=OE-OF,可先求出B点坐标,即可得出OE,OA′的长,如果设OF=x,那么A′F=OE-x,可在直角三角形A′OF中,用勾股定理求出x即OF的长;
(3)根据直线MN的解析式可知:三角形MON是等腰直角三角形,那么∠NMO=45°,如果过G作x轴的垂线,不难得出MG=
| 2 |
| 2 |
解答:解:(1)由题可知:D(2,2),
因为点D在反比例函数y=
(k>0)上,
所以k=4,
∴y=
(2)B点的坐标为(1,4),可知△EBF≌△A'OF,
设OF=x,则EF=A'F=4-x,
在直角三角形A′OF中,A′F2+A′O2=OF2,
∴(4-x)2+1=x2
解得:x=
;
(3)MG•NH的值不变,且值为8.
由y=-x+3得:OM=ON
∴∠OMN=∠ONM=45°
∴MG=
PQ,NH=
PR
∴MG•NH=2PQ•PR=8.
因为点D在反比例函数y=
| k |
| x |
所以k=4,
∴y=
| 4 |
| x |
(2)B点的坐标为(1,4),可知△EBF≌△A'OF,
设OF=x,则EF=A'F=4-x,
在直角三角形A′OF中,A′F2+A′O2=OF2,
∴(4-x)2+1=x2
解得:x=
| 17 |
| 8 |
(3)MG•NH的值不变,且值为8.
由y=-x+3得:OM=ON
∴∠OMN=∠ONM=45°
∴MG=
| 2 |
| 2 |
∴MG•NH=2PQ•PR=8.
点评:本题主要考查了反比例函数的应用、等腰三角形的判定和性质等知识点.利用数形结合解决此类问题,是非常有效的方法.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
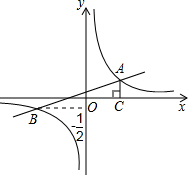 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
 的图象上,△ODC是以CO为斜边的等腰直角三角形,且C (4,0).
的图象上,△ODC是以CO为斜边的等腰直角三角形,且C (4,0). 上,求点D1的坐标;
上,求点D1的坐标;
 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数 (m≠0)的图象相交于A、B两点,且点B的纵坐标为
(m≠0)的图象相交于A、B两点,且点B的纵坐标为 ,过点A作AC⊥x轴于点C,AC=1,OC=2.
,过点A作AC⊥x轴于点C,AC=1,OC=2. (x>0)的图像 上运动,那么点B在函数 (填函数解析式)的图像上运动.
(x>0)的图像 上运动,那么点B在函数 (填函数解析式)的图像上运动.