题目内容
解下列方程:
(1)(x+4)2=5(x+4)
(2)4x2-12x-7=0(配方法)
(3) .
.
解:(1)由原方程移项,得
(x+4)2-5(x+4)=0
∴(x+4)(x+4-5)=0,即(x+4)(x-1)=0,
∴x+4=0或x-1=0,
解得x=-4或x=1;
(2)由原方程,得
4x2-12x=7,
化二次项系数为1,得
∴x2-3x= ,
,
等式的两边同时加上一次项系数的一半的平方,得
x2-3x+ =
= +
+ ,
,
即(x- )2=4,
)2=4,
∴x1= ,x2=
,x2= ;
;
(3)设 =y,则由原方程,得
=y,则由原方程,得
y2+5y-6=0,
∴(y-1)(y+6)=0
∴y-1=0或y+6=0,
解得,y=1或y=-6;
①当y=1时, =1,即x=x+1,
=1,即x=x+1,
∴无解;
②当y=-6时, =-6,
=-6,
解得,x=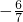 ,经检验,x=
,经检验,x=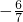 是原方程的解.
是原方程的解.
分析:(1)利用因式分解法解方程;
(2)利用配方法解方程;
(3)利用换元法解方程.
点评:本题综合考查了因式分解法、配方法、换元法解一元二次方程.解分式方程时,一定要验根.
(x+4)2-5(x+4)=0
∴(x+4)(x+4-5)=0,即(x+4)(x-1)=0,
∴x+4=0或x-1=0,
解得x=-4或x=1;
(2)由原方程,得
4x2-12x=7,
化二次项系数为1,得
∴x2-3x=
 ,
,等式的两边同时加上一次项系数的一半的平方,得
x2-3x+
 =
= +
+ ,
,即(x-
 )2=4,
)2=4,∴x1=
 ,x2=
,x2= ;
;(3)设
 =y,则由原方程,得
=y,则由原方程,得y2+5y-6=0,
∴(y-1)(y+6)=0
∴y-1=0或y+6=0,
解得,y=1或y=-6;
①当y=1时,
 =1,即x=x+1,
=1,即x=x+1,∴无解;
②当y=-6时,
 =-6,
=-6,解得,x=
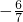 ,经检验,x=
,经检验,x=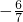 是原方程的解.
是原方程的解.分析:(1)利用因式分解法解方程;
(2)利用配方法解方程;
(3)利用换元法解方程.
点评:本题综合考查了因式分解法、配方法、换元法解一元二次方程.解分式方程时,一定要验根.

练习册系列答案
相关题目