题目内容
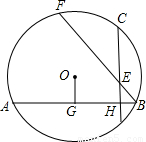
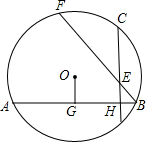 如图⊙O的弦AB⊥CD于H,D、E关于AB对称,BE延长线交⊙O于F,连接FC,作OG⊥AB于G,则下列结论:①FC=CE,②
如图⊙O的弦AB⊥CD于H,D、E关于AB对称,BE延长线交⊙O于F,连接FC,作OG⊥AB于G,则下列结论:①FC=CE,② |
| AF |
 |
| AD |
| A、①②③ | B、①②④ |
| C、②③④ | D、①②③④ |
分析:①连接FC,BD,先证∠BDE=∠BED,进而证得∠CFE=∠CEF,所以可得FC=CE.
②连接AC,由于∠ABE+∠BED=90°,∠A+∠ACH=90°,根据①的结论,∠A=∠DEB,所以∠B=∠ACH,所以它们所对的弧相等.
③由②知,不正确.
④由②可以证得△ECF∽△BED.
②连接AC,由于∠ABE+∠BED=90°,∠A+∠ACH=90°,根据①的结论,∠A=∠DEB,所以∠B=∠ACH,所以它们所对的弧相等.
③由②知,不正确.
④由②可以证得△ECF∽△BED.
解答: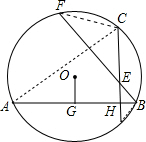 解:连接FC,BD,AC,
解:连接FC,BD,AC,
∵D、E关于AB对称,
∴∠BDE=∠BED,
又∠CFE=∠BDE,
∴∠CFE=∠CEF,
∴△ECF∽△EBD.故④正确.
∴FC=CE.故①正确.
∠ABE+∠BED=90°,∠A+∠ACH=90°,
∵∠A=∠EDB,
∴∠ABF=∠ACD,
∴
=
.故②正确.
∵∠EBD≠90°,
∴∠B≠∠BEH.故③错误.
故选B.
 解:连接FC,BD,AC,
解:连接FC,BD,AC,∵D、E关于AB对称,
∴∠BDE=∠BED,
又∠CFE=∠BDE,
∴∠CFE=∠CEF,
∴△ECF∽△EBD.故④正确.
∴FC=CE.故①正确.
∠ABE+∠BED=90°,∠A+∠ACH=90°,
∵∠A=∠EDB,
∴∠ABF=∠ACD,
∴
 |
| AF |
 |
| AD |
∵∠EBD≠90°,
∴∠B≠∠BEH.故③错误.
故选B.
点评:此题综合运用了等角的余角相等,圆周角定理等.以及利用圆周角定理的结论证明相似等.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
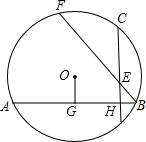 如图⊙O的弦AB⊥CD于H,D、E关于AB对称,BE延长线交⊙O于F,连接FC,作OG⊥AB于G,则下列结论:①FC=CE,②
如图⊙O的弦AB⊥CD于H,D、E关于AB对称,BE延长线交⊙O于F,连接FC,作OG⊥AB于G,则下列结论:①FC=CE,②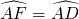 ,③∠B=∠BEH,④△ECF∽△EBD,成立的是
,③∠B=∠BEH,④△ECF∽△EBD,成立的是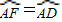 ,③∠B=∠BEH,④△ECF∽△EBD,成立的是( )
,③∠B=∠BEH,④△ECF∽△EBD,成立的是( )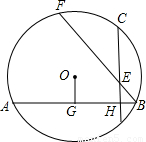
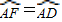 ,③∠B=∠BEH,④△ECF∽△EBD,成立的是( )
,③∠B=∠BEH,④△ECF∽△EBD,成立的是( )