题目内容
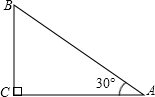如图Rt△ABC中，∠A=30°，AB+BC=12 cm，则AB=________cm．
8
分析：此题考查了直角三角形的性质、勾股定理，利用直角三角形的性质和勾股定理求解．
解答：∵Rt△ABC中，∠A=30°，
∴BC=
AB．
设AB=xcm，
则有BC=（12-x）cm，AB=2xcm
∵AB2=AC2+BC2
∴AB=8cm．
点评：熟记30°角所对的直角边是斜边的一半，解题时还要注意方程思想的应用．
分析：此题考查了直角三角形的性质、勾股定理，利用直角三角形的性质和勾股定理求解．
解答：∵Rt△ABC中，∠A=30°，
∴BC=
AB．设AB=xcm，
则有BC=（12-x）cm，AB=2xcm
∵AB2=AC2+BC2
∴AB=8cm．
点评：熟记30°角所对的直角边是斜边的一半，解题时还要注意方程思想的应用．
练习册系列答案
优学名师名题系列答案
相关题目
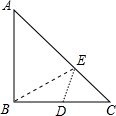如图Rt△ABC中，AB=BC=4，D为BC的中点，在AC边上存在一点E，连接ED，EB，则△BDE周长的最小值为（ ）A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
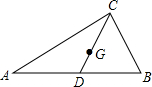如图Rt△ABC中，∠C=90°，AC=8，BC=6，CD为AB边上的中线，点G是重心，则DG=
如图Rt△ABC中，∠C=90°，AC=12cm，BC=6cm，点P从B出发，以1cm/s的速度向C运动，同时点Q从C出发，以1cm/s的速度向A运动，问几秒时PQ的长为2
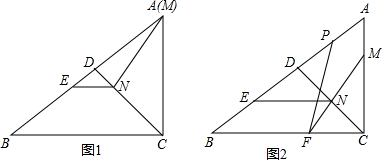
已知：如图Rt△ABC中，∠C=Rt∠，AB=5，BC=4．