题目内容
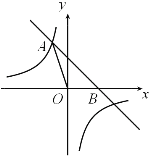
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于点A(a,3),且与x轴相交于点B.
的图象相交于点A(a,3),且与x轴相交于点B.
(1)求该反比例函数的表达式;
(2)若P为y轴上的点,且△AOP的面积是△AOB的面积的![]() ,请求出点P的坐标.
,请求出点P的坐标.
(3)写出直线![]() 向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标。
向下平移2个单位的直线解析式,并求出这条直线与双曲线的交点坐标。
【答案】(1)、y=-![]() ;(2)、P(0,4)或(0,-4);(3)、(
;(2)、P(0,4)或(0,-4);(3)、(![]() ,
,![]() )、(-
)、(-![]() ,-
,-![]() )
)
【解析】
试题分析:(1)、首先根据一次函数求出点A的坐标,然后得出反比例函数的坐标;(2)、首先得出OB的长度,然后设点P的坐标为(0,y),然后根据三角形的面积关系求出y的值,得出点P的坐标;(3)、首先得出平移后的直线解析式,然后求出交点坐标.
试题解析:(1)、∵点A(a,3)在直线y=-x+2 上,
∴ 3=-a +2.∴ a =-1.
∴A(-1,3).
∵点A(-1,3)在反比例函数y=![]() 的图象上,
的图象上,
∴3=![]() .
.
∴ k = -3.
∴y=-![]() .
.
(2)、在直线y=-x+2中,令y=0,得:x=2,
∴OB=2,设P(0,y),
∵![]() ,
,
∴![]() ,
,
∴![]() ,∴y=±4,
,∴y=±4,
∴P(0,4 )或P(0,-4 ).
(3)、平移后的直线解析式为y=-x,则-x=-![]() ,解得:x=±
,解得:x=±![]()
∴交点坐标为(![]() ,
,![]() )、(-
)、(-![]() ,-
,-![]() ).
).

练习册系列答案
相关题目