题目内容
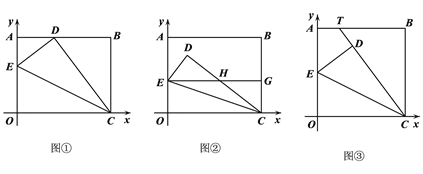
【题目】如图,矩形ABCD中,AB=12,AD=9,E为BC上一点,且BE=4,动点F从点A出发沿射线AB方向以每秒3个单位的速度运动.连结DF,DE, EF. 过点E作DF的平行线交射线AB于点H,设点F的运动时间为t(不考虑D、E、F在一条直线上的情况).

(1) 填空:当t= 时,AF=CE,此时BH= ;
(2)当△BEF与△BEH相似时,求t的值;
(3)当F在线段AB上时,设△DEF的面积为S,△DEF的周长为C.
① 求S关于t的函数关系式;
② 直接写出周长C的最小值.

【答案】(1) ![]() 、
、![]() ;(2)
;(2)![]() ;(3)①
;(3)① ![]() ;②
;② ![]() .
.
【解析】
(1)在Rt△ABC中,利用勾股定理可求得AB的长,即可得到AD、t的值,从而确定AE的长,由DE=AE-AD即可得解.
(2)若△DEG与△ACB相似,要分两种情况:①AG:DE=DH:GE,②AH:EG=DH:DE,根据这些比例线段即可求得t的值.(需注意的是在求DE的表达式时,要分AD>AE和AD<AE两种情况);
(3)分别表示出线段FD和线段AD的长,利用面积公式列出函数关系式即可.
(1)∵BC=AD=9,BE=4,
∴CE=9-4=5,
∵AF=CE,
即:3t=5,
∴t=![]() ,
,
∴![]() ,
,
即:![]() ,
,
解得BH=![]() ;
;
当t=![]() 时,AF=CE,此时BH=
时,AF=CE,此时BH=![]() .
.
(2)由EH∥DF得∠AFD=∠BHE,又∵∠A=∠CBH=90°
∴△EBH∽△DAF ∴![]() 即
即![]() ∴BH=
∴BH=![]()
当点F在点B的左边时,即t<4时,BF=12-3t
此时,当△BEF∽△BHE时:![]() 即
即![]() 解得:
解得:![]()
此时,当△BEF∽△BEH时: 有BF=BH, 即![]() 解得:
解得:![]()
当点F在点B的右边时,即t>4时,BF=3t-12
此时,当△BEF∽△BHE时:![]() 即
即![]() 解得:
解得:![]()
(3)① ∵EH∥DF
∴△DFE的面积=△DFH的面积=![]() ;
;
② 如图

∵BE=4,
∴CE=5,根据勾股定理得,DE=13,是定值,
所以当C最小时DE+EF最小,作点E关于AB的对称点E'
连接DE,此时DE+EF最小,
在Rt△CDE'中,CD=12,CE'=BC+BE'=BC+BE=13,
根据勾股定理得,DE'=![]() ,
,
∴C的最小值=![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案