题目内容
 如图为住宅区内的两幢楼,它们的高AB=CD=30m,现需了解甲楼对乙楼的采光的影响情况.当太阳光与水平线的夹角为30°时.试求:
如图为住宅区内的两幢楼,它们的高AB=CD=30m,现需了解甲楼对乙楼的采光的影响情况.当太阳光与水平线的夹角为30°时.试求:(1)若两楼间的距离AC=24m时,甲楼的影子,落在乙楼上有多高?
(2)若甲楼的影子,刚好不影响乙楼,那么两楼的距离应当有多远?
分析:(1)首先设太阳光与CD的交点为E,连接BD,易得四边形ABD是矩形,然后在Rt△BDE中,由DE=BD•tan30°即可求得答案;
(2)首先根据题意可得当太阳光照射到点C时,甲楼的影子,刚好不影响乙楼,然后由AC=
,即可求得答案.
(2)首先根据题意可得当太阳光照射到点C时,甲楼的影子,刚好不影响乙楼,然后由AC=
| AB |
| tan30° |
解答: 解:(1)设太阳光与CD的交点为E,连接BD,
解:(1)设太阳光与CD的交点为E,连接BD,
∵AB=CD=30m,BA⊥AC,CD⊥AC,
∴四边形ABCD是矩形,
∴BD=AC=24m,∠BDE=90°,
∵∠DBE=30°,
∴在Rt△BDE中,DE=BD•tan30°=24×
=8
(m),
∴EC=CD-DE=30-8
(m).
 答:甲楼的影子,落在乙楼上有(30-8
答:甲楼的影子,落在乙楼上有(30-8
)m高;
(2)如图:当太阳光照射到点C时,甲楼的影子,刚好不影响乙楼,
在Rt△ABC中,AB=30m,∠ACB=30°,
∴AC=
=30÷
=30
(m).
答:两楼的距离应当为30
m.
 解:(1)设太阳光与CD的交点为E,连接BD,
解:(1)设太阳光与CD的交点为E,连接BD,∵AB=CD=30m,BA⊥AC,CD⊥AC,
∴四边形ABCD是矩形,
∴BD=AC=24m,∠BDE=90°,
∵∠DBE=30°,
∴在Rt△BDE中,DE=BD•tan30°=24×
| ||
| 3 |
| 3 |
∴EC=CD-DE=30-8
| 3 |
 答:甲楼的影子,落在乙楼上有(30-8
答:甲楼的影子,落在乙楼上有(30-8| 3 |
(2)如图:当太阳光照射到点C时,甲楼的影子,刚好不影响乙楼,
在Rt△ABC中,AB=30m,∠ACB=30°,
∴AC=
| AB |
| tan30° |
| ||
| 3 |
| 3 |
答:两楼的距离应当为30
| 3 |
点评:此题考查了解直角三角形的应用.此题难度适中,注意能根据题意构造直角三角形,并能借助于解直角三角形的知识求解是解此题的关键.

练习册系列答案
相关题目
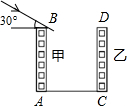 如图为住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=24m,现需了解甲楼对乙楼采光的影响情况.当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?
如图为住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=24m,现需了解甲楼对乙楼采光的影响情况.当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高? 如图为住宅区内的两幢楼;它们的高AB=CD=30m,两楼间的距离AC=24m,现需了解南楼对北楼的采光的影响情况,经测量发现南楼的影子落在北楼上有16.2m,问此时太阳光线与水平线的夹角的度数.
如图为住宅区内的两幢楼;它们的高AB=CD=30m,两楼间的距离AC=24m,现需了解南楼对北楼的采光的影响情况,经测量发现南楼的影子落在北楼上有16.2m,问此时太阳光线与水平线的夹角的度数. ≈1.41,
≈1.41, ≈1.73)?
≈1.73)?
