题目内容
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,AD是BC边上的高,点E、F分别是AB边和AC边上的动点,且∠EDF=90°.
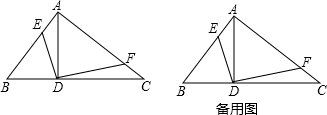
(1)求DE:DF的值;
(2)连结EF,设点B与点E间的距离为x,△DEF的面积为y,求y关于x的函数解析式,并写出x的取值范围.
解:(1)∵∠BAC=90°,
∴∠B+∠C=90°,
∵AD是BC边上的高,
∴∠DAC+∠C=90°,
∴∠B=∠DAC
又∵∠EDF=90°,
∴∠BDE+∠EDA=∠ADF+∠EDA=90°,
∴∠BDE=∠ADF,
∴△BED∽△AFD,
∴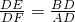 ,
,
∵tanB=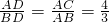 ,
,
∴DE:DF= ;
;
(2)由△BED∽△AFD,得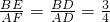 ,
,
∴AF= BE=
BE= x,
x,
∵BE=x,
∴AE=3-x,
∵∠BAC=90°,
∴EF2=(3-x)2+( x)2=
x)2= x2-6x+9,
x2-6x+9,
∵DE:DF=3:4,∠EDF=90°,
∴ED= EF,FD=
EF,FD= EF,
EF,
∴y= ED•FD=
ED•FD=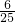 EF2,
EF2,
∴y= x2-
x2-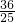 x+
x+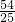 (0≤x≤3).
(0≤x≤3).
分析:(1)由在△ABC中,∠BAC=90°,AD是BC边上的高,易证得△BED∽△AFD,然后由相似三角形的对应边成比例,即可求得答案;
(2)由勾股定理易得EF2=(3-x)2+( x)2=
x)2= x2-6x+9,又由DE:DF=3:4,∠EDF=90°,即可求得答案.
x2-6x+9,又由DE:DF=3:4,∠EDF=90°,即可求得答案.
点评:此题考查了相似三角形的判定与性质、勾股定理以及直角三角形的性质.此题难度较大,注意掌握方程思想与数形结合思想的应用.
∴∠B+∠C=90°,
∵AD是BC边上的高,
∴∠DAC+∠C=90°,
∴∠B=∠DAC
又∵∠EDF=90°,
∴∠BDE+∠EDA=∠ADF+∠EDA=90°,
∴∠BDE=∠ADF,
∴△BED∽△AFD,
∴
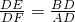 ,
,∵tanB=
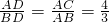 ,
,∴DE:DF=
 ;
; (2)由△BED∽△AFD,得
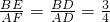 ,
,∴AF=
 BE=
BE= x,
x,∵BE=x,
∴AE=3-x,
∵∠BAC=90°,
∴EF2=(3-x)2+(
 x)2=
x)2= x2-6x+9,
x2-6x+9,∵DE:DF=3:4,∠EDF=90°,
∴ED=
 EF,FD=
EF,FD= EF,
EF,∴y=
 ED•FD=
ED•FD=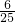 EF2,
EF2,∴y=
 x2-
x2-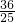 x+
x+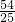 (0≤x≤3).
(0≤x≤3). 分析:(1)由在△ABC中,∠BAC=90°,AD是BC边上的高,易证得△BED∽△AFD,然后由相似三角形的对应边成比例,即可求得答案;
(2)由勾股定理易得EF2=(3-x)2+(
 x)2=
x)2= x2-6x+9,又由DE:DF=3:4,∠EDF=90°,即可求得答案.
x2-6x+9,又由DE:DF=3:4,∠EDF=90°,即可求得答案.点评:此题考查了相似三角形的判定与性质、勾股定理以及直角三角形的性质.此题难度较大,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=