题目内容
17.在Rt△ABC中,∠C=90°,由下列条件解直角三角形:(1)已知BC=6$\sqrt{15}$,AC=6$\sqrt{5}$,求AB;
(2)已知BC=20,AB=20$\sqrt{2}$,求∠B;
(3)已知AB=30,∠A=60°,求AC;
(4)已知AC=15,∠A=30°,求BC.
分析 (1)利用勾股定理列式求出AB即可;
(2)利用∠B的余弦求出∠B即可;
(3)利用∠A的余弦求出∠A即可;
(4)利用∠A的正切求出∠A即可.
解答 解:(1)由勾股定理得,AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{(6\sqrt{15})^{2}+(6\sqrt{5})^{2}}$=12$\sqrt{5}$,
(2)∵cos∠B=$\frac{BC}{AB}=\frac{20}{20\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴∠B=45°;
(3)∵cos∠A=$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$,
∵AB=30,
∴AC=15$\sqrt{3}$;
(4)∵tan∠A=$\frac{BC}{AC}$=$\frac{\sqrt{3}}{3}$,AC=15,
∴BC=5$\sqrt{3}$.
点评 本题考查了解直角三角形,主要利用了锐角三角函数和勾股定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.($\frac{2}{3}$)2014•(-1.5)2015=( )
| A. | ($\frac{2}{3}$)2014 | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | (-$\frac{3}{2}$)2014 |
6.已知$\frac{2a}{3b+3c}$=$\frac{2b}{3c+3a}$=$\frac{2c}{3a+3b}$=k,则k的值为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{1}{3}$或-$\frac{2}{3}$ | D. | $\frac{2}{3}$或-1 |
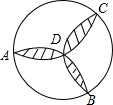 小明把如图所示的圆形纸板(点A,B,C是圆的三等分点)挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则投中阴影区域的概率是1-$\frac{3\sqrt{3}}{2π}$.
小明把如图所示的圆形纸板(点A,B,C是圆的三等分点)挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则投中阴影区域的概率是1-$\frac{3\sqrt{3}}{2π}$. 如图,在安大公路(直线BD)的同侧有两个气象信息采集点A、E,点A、E到安大公路的距离AB=12、ED=3,两垂足间的距离BD=20.
如图,在安大公路(直线BD)的同侧有两个气象信息采集点A、E,点A、E到安大公路的距离AB=12、ED=3,两垂足间的距离BD=20.