题目内容
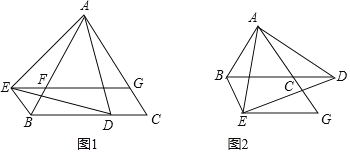
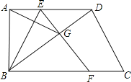
【题目】已知:如图,在四边形![]() 中,
中,![]() ,
,![]() .点
.点![]() 为边
为边![]() 上一点,将
上一点,将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在四边形对角线
落在四边形对角线![]() 上的点
上的点![]() 处,
处,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .
.
![]() 点
点![]() 可以是
可以是![]() 的中点吗?请说明理由;
的中点吗?请说明理由;
![]() 求证:
求证:![]() ;
;
![]() 设
设![]() ,
,![]() ,
,![]() .当四边形
.当四边形![]() 为平行四边形时,求
为平行四边形时,求![]() ,
,![]() ,
,![]() 应满足的关系.
应满足的关系.
【答案】(1)点![]() 不可以是
不可以是![]() 的中点;理由见解析;(2)见解析;(3)
的中点;理由见解析;(2)见解析;(3)![]() .理由见解析.
.理由见解析.
【解析】
(1)在直角三角形中比较斜边直角边即可,(2)由![]() 得
得![]() 进而证明
进而证明![]() 推出
推出![]() ,在等腰
,在等腰![]() 得到
得到![]() ,即可证明三角形相似,(3)由
,即可证明三角形相似,(3)由![]() ,证明
,证明![]() ,推出
,推出![]() 证明
证明![]() 列出比例式
列出比例式![]() ,即可解题.
,即可解题.
![]() 解:点
解:点![]() 不可以是
不可以是![]() 的中点;理由如下:
的中点;理由如下:
根据题意得:![]() ,
,![]() ,
,
∴![]() 中,
中,![]() ,
,
∴![]() ,
,
因此点![]() 不可以是
不可以是![]() 的中点.
的中点.
![]() 证明:∵
证明:∵![]()
![]()
∵![]() 沿直线
沿直线![]() 折叠,
折叠,
∴![]()
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() 为等腰三角形.
为等腰三角形.
∵![]() ,
,![]() ,
,
∴![]() ,
,
![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
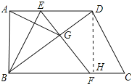
![]() 解:
解:![]() .理由如下:
.理由如下:
过点![]() 作
作![]() ,如图所示:
,如图所示:
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目