题目内容
抛物线y=2（x-5）（x+3）与x轴两交点之间的距离为
- A.8
- B.16
- C.5
- D.3
A
分析：由题意令y=0，得方程2（x-5）（x+3）=0，求出方程的两根，即为抛物线与x轴的交点，从而求出抛物线与x轴两交点之间的距离．
解答：令y=0得方程，
2（x-5）（x+3）=0，
解得x=5或-3，
∴抛物线y=2（x-5）（x+3）与x轴的交点为：（5，0），（-3，0），
∴抛物线y=2（x-5）（x+3）与x轴两交点之间的距离为：|-3-5|=8，
故选A．
点评：此题主要考查抛物线的基本性质，解题的关键是求出抛物线与x轴的交点，把函数的方程结合起来出题，是一种比较好的题型．
分析：由题意令y=0，得方程2（x-5）（x+3）=0，求出方程的两根，即为抛物线与x轴的交点，从而求出抛物线与x轴两交点之间的距离．
解答：令y=0得方程，
2（x-5）（x+3）=0，
解得x=5或-3，
∴抛物线y=2（x-5）（x+3）与x轴的交点为：（5，0），（-3，0），
∴抛物线y=2（x-5）（x+3）与x轴两交点之间的距离为：|-3-5|=8，
故选A．
点评：此题主要考查抛物线的基本性质，解题的关键是求出抛物线与x轴的交点，把函数的方程结合起来出题，是一种比较好的题型．
练习册系列答案
相关题目
A和C，和x轴的另一个交点为B．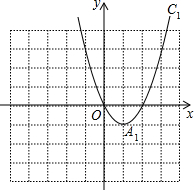
已知抛物线C1：y=x2-2x的图象如图所示，把C1的图象沿y轴翻折，得到抛物线C2的图象，抛物线C1与抛物线C2的图象合称图象C3．