题目内容
如图:已知在正方形ABCD中,E是边AB的中点,点F在BC上,且∠ADE=∠FDE。

(1)求证:DF=AB+FB;
(2)以E为圆心EB为半径作⊙E,试判断⊙E与直线DF的位置关系,并说明理由;
(3)在⑵的条件下,若CD=4cm,点M在线段DF上从点D出发向点F运动,速度为0.5cm/s,以M为圆心,MD为半径作⊙M。当运动时间为多少秒时,⊙M与⊙E相切?
【答案】
(1)证明见解析;(2)相切,理由见解析;(3) .
.
【解析】
试题分析:(1)过E点作EP⊥DF,垂足为P,连接EF,易证△DAE≌△DPE,△EPF≌△EBF,即有:AD=AP,BF=PF,而AB=AD,从而得证;
(2)由EB=EP知⊙E与直线DF相切;
(3)设t秒后两圆相切,利用勾股定理得出方程,解方程即可求解.
试题解析:(1)过E点作EP⊥DF,垂足为P,连接EF,

在△DAE和△DPE中
∵∠ADE=∠FDE
DE=DE
∠DAE=∠DPE
∴△DAE≌△DPE,
∴DP=DA,AE=EP
又DA=AB
∴DP=AB
∵E为AB的中点
∴BE=AE=EP
在Rt△EPF和Rt△EBF中
BE=PE
EF=EF
∴Rt△EPF≌Rt△EBF
∴BF=PF
∴DF=DP+PF=AB+BF
(2)由(1)知:EP=EB
故⊙E与直线DF相切.
(3)设t秒后⊙M与⊙E相切,则有:
(4-0.5t)2+22=(2+0.5t)2
解得:t= .
.
考点: 1.全等三角形的判定与性质;2.勾股定理;3.圆和圆的位置关系.

练习册系列答案
相关题目
 18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.
18、如图,已知在正方形ABCD中,P是BC上的一点,且AP=DP.求证:P是BC中点.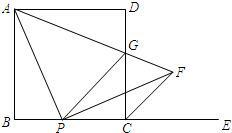 一点,连接AP.过点P作PF⊥AP,与∠DCE的平分线CF相交于点F.连接AF,与边CD相交于点G,连接PG.
一点,连接AP.过点P作PF⊥AP,与∠DCE的平分线CF相交于点F.连接AF,与边CD相交于点G,连接PG. 如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=
如图,已知在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB= (2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点.
(2013•仓山区模拟)如图,已知在正方形ABCD网格中,每个小方格都是边长为1的正方形,E是边DC上的一个网格的格点. (2010•郑州模拟)如图,已知在正方形ABCD中,EF分别是AB,BC上的点,若有AE+CF=EF,请你猜想∠EDF的度数,并说明理由.
(2010•郑州模拟)如图,已知在正方形ABCD中,EF分别是AB,BC上的点,若有AE+CF=EF,请你猜想∠EDF的度数,并说明理由.