题目内容
如图,在一个矩形空地ABCD上修建一个矩形花坛AMPQ,要求点M在AB上,点Q在AD上,点P在对角线BD上.若AB=6 m,AD=4 m,设AM的长为x m,矩形AMPQ的面积为S平方米.

(1)求S与x的函数关系式;
(2)当x为何值时,S有最大值?请求出最大值.
答案:
解析:
解析:
|
(1)∵四边形AMPQ是矩形, ∴PQ=AM=x.(1分) ∵PQ∥AB, ∴△PQD∽△BAD.(3分) ∴ ∵AB=6,AD=4, ∴DQ= ∴AQ=4- ∴S=AQ·AM=(4- (注:不写自变量取值范围不扣分,若写错则扣1分) (2)解法一:∵S=- 又- ∴S有最大值. ∴当x=3时,S的最大值为6.(11分) 答:当AM的长为3米时,矩形AMPQ的面积最大;最大面积为6平方米.(12分) 解法二:∵- ∴S有最大值.(8分) ∴当x=- S有最大值为- 答:当AM的长为3米时,矩形AMPQ的面积最大;最大面积为6平方米.(12分) |

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
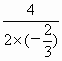 =3时,
=3时, 线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米.
线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米. 线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米.
线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米.
