题目内容
阅读材料：设一元二次方程ax2+bx+c=0（a≠0）的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2=-| b |
| a |
| c |
| a |
根据该材料填空：已知x1，x2是方程x2+6x+3=0的两实数根，则
| x2 |
| x1 |
| x1 |
| x2 |
分析：根据一元二次方程根与系数的关系，可以求得两根之积或两根之和，根据
+
=
=
，代入数值计算即可．
| x2 |
| x1 |
| x1 |
| x2 |
| x22+x12 |
| x1．x2 |
| (x1+x2)2-2x1．x2 |
| x1．x2 |
解答：解：由题意知，x1+x2=-
=-6，x1x2=3，
所以
+
=
=
=
=10．
| b |
| a |
所以
| x2 |
| x1 |
| x1 |
| x2 |
| x22+x12 |
| x1．x2 |
| (x1+x2)2-2x1．x2 |
| x1．x2 |
| (-6)2-2×3 |
| 3 |
点评：本题考查了代数式变形，难度中等，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
20、阅读材料，解答问题．
（1）阅读材料：设一元二次方程ax2+bx+c=0（a≠0）的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2=-
，x1•x2=
．
根据该材料：已知x1、x2是方程x2+6x+3=0的两实数根，求
+
的值．
（2）已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 2 | 1 | 2 | … |
（1）阅读材料：设一元二次方程ax2+bx+c=0（a≠0）的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2=-
，x1•x2=
．
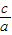根据该材料：已知x1、x2是方程x2+6x+3=0的两实数根，求
+
的值．
（2）已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
点A（x1，y1）、B（x2，y2）在函数的图象上，当0＜x1＜1，2＜x2＜3时，试判断y1与y2的大小关系．
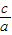，x1•x2=．根据该材料：已知x1、x2是方程x2+6x+3=0的两实数根，求
+的值．（2）已知二次函数y=ax2+bx+c中，其函数y与自变量x之间的部分对应值如下表所示：
| x | … | 1 | 2 | 3 | … | |
| y | … | 5 | 2 | 1 | 2 | … |