题目内容
 如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN=45°,连结AM、AN,并延长分别交BC、CD于E、F两点,则∠CME+∠CNF=________.
如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN=45°,连结AM、AN,并延长分别交BC、CD于E、F两点,则∠CME+∠CNF=________.
90°
分析:由BD为正方形ABCD的对角线,可得∠1=∠3,∠2=∠4,然后用∠1和∠2表示∠MCN以及∠EMC+∠FNC,即可求得答案.
解答:∵BD为正方形ABCD的对角线,
∴△AMN与△CMN关于BD对称,
∴∠1=∠3,∠2=∠4,
∴∠EMC=180°-∠1-∠3=180°-2∠1.
同理∠FNC=180°-2∠2.
∴∠EMC+∠FNC=360°-2(∠1+∠2).
∵∠MCN=180°-(∠1+∠2),
∴∠EMC+∠FNC=2∠MCN=2×45°=90°.
故答案为:90°.
点评:此题考查了正方形的性质.此题难度适中,注意正确用∠1和∠2表示∠MCN以及∠EMC+∠FNC是关键.
分析:由BD为正方形ABCD的对角线,可得∠1=∠3,∠2=∠4,然后用∠1和∠2表示∠MCN以及∠EMC+∠FNC,即可求得答案.
解答:∵BD为正方形ABCD的对角线,
∴△AMN与△CMN关于BD对称,
∴∠1=∠3,∠2=∠4,
∴∠EMC=180°-∠1-∠3=180°-2∠1.
同理∠FNC=180°-2∠2.
∴∠EMC+∠FNC=360°-2(∠1+∠2).
∵∠MCN=180°-(∠1+∠2),
∴∠EMC+∠FNC=2∠MCN=2×45°=90°.
故答案为:90°.
点评:此题考查了正方形的性质.此题难度适中,注意正确用∠1和∠2表示∠MCN以及∠EMC+∠FNC是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
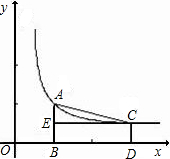 如图,已知A、C两点在双曲线y=
如图,已知A、C两点在双曲线y= (2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是
(2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是 如图,已知A、B两点的坐标分别为(
如图,已知A、B两点的坐标分别为( 如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.
如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论. 如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.
如图,已知E、F两点在线段BC上,AB=AC,BF=CE,你能判断线段AF和AE的大小关系吗?说明理由.