Question

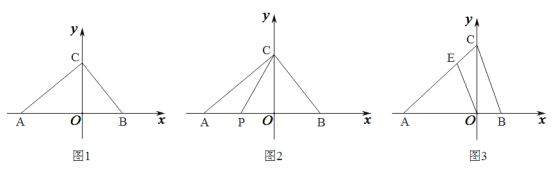
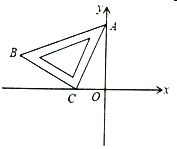
【题目】如图，将一块等腰直角三角板放置在平面直角坐标系中，，，点在轴的正半轴上，点在轴的负半轴上，点在第二象限，所在直线的函数表达式是，若保持的长不变，当点在轴的正半轴滑动，点随之在轴的负半轴上滑动，则在滑动过程中，点与原点的最大距离是__________．

Answer 1

【答案】

【解析】

首先取AC的中点E，连接BE，OE，OB，可求得OE与BE的长，然后由三角形三边关系，求得点B到原点的最大距离.

当x=0时，y=2x+4=4,则A（0，4）;

当y=0时，x=-2, 则C（-2，0）.

∴OA=4，OC=2，

AC=

如图所示:

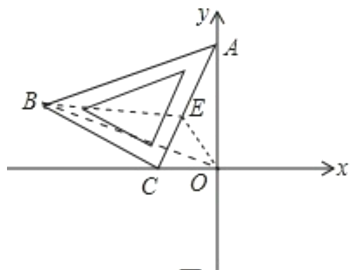
取AC的中点E，连接BE，OE，OB，

∴∠AOC=90°，AC=，

OE=CE=AC=

∴BC⊥AC，BC=，

∴BE=，

若点O，E，B不在一条直线上，则

OB<OE+BE=5+

若点O，E、B在一条直线上，则

OB=OE+BE=5+，

当O，E，B三点在一条直线上时，OB取得

最大值，最大值为5+，

故答案为: .