题目内容
已知:点P是三角形ABC内任意一点,连接PA、PB、PC.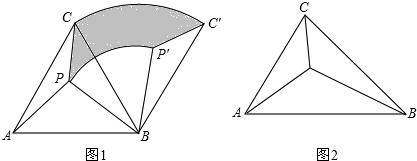
(1)如图1,当△ABC是等边三角形时,将△PBC绕点B顺时针旋转60°到△P′BC′的位置.若AB的长为a,BP的长为b(b<a),求△PBC旋转到△P′BC′的过程中边PC所扫过区域(图1中阴影部分)的面积.(用a、b表示)
(2)如图2,若△ABC为任意锐角三角形,问:当∠APC、∠APB和∠BPC满足什么大小关系时,AP+BP+CP的和最小,并说明理由.
 解:(1)∵△ABC是等边三角形,AB的长为a,
解:(1)∵△ABC是等边三角形,AB的长为a,∴AB=BC=a.
又∵△P′BC′是由△PBC绕点B顺时针旋转60°得到的,
∴∠PBP′=∠CBC′=60°,
∴S阴影=
 -
- =
= π(a2-b2);
π(a2-b2);(2)如图,将△BPC绕着点B顺时针旋转60°到△BP′C′的位置,连接PP′.
则△BPC≌△BP′C′,∠PBP′=60°,
∴BP=BP′,
∴△BPP′为等边三角形,
∴∠BPP′=∠BP′P=60°,PP′=BP,C′P′=CP,
则AP+BP+CP=AP+PP′+P′C′≥AC′,
显然当A、P、P′、C′四点在同一直线上时,AP+BP+CP有最小值,
此时,∠APB=120°,∠BP′C′=120°,
于是∠BPC=∠BP′C′=120°,∠APC=360°-2×120°=120°,
∴当∠APC=∠BPC=∠APB=120°时,AP+BP+CP的和最小.
分析:(1)根据旋转变换的性质可得阴影部分的面积等于以BC为半径的扇形面积减去以BP为半径的扇形的面积,然后列式进行计算即可得解;
(2)如图,将△BPC绕着点B顺时针旋转60°到△BP′C′的位置,连接PP′.通过旋转,使A、P、P′、C′四点共线,这样AP+BP+CP的和最小.
点评:本题考查了旋转的性质,等边三角形的判定与性质以及扇形的面积公式等知识点.观察出阴影部分的面积的表示是解答(1)题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 22、已知A点坐标是(-2,2).
22、已知A点坐标是(-2,2).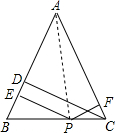 【老题重现】
【老题重现】

 已知:点D是△ABC的边BC的中点,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F.
已知:点D是△ABC的边BC的中点,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F. 已知:点D是等边△ABC边上任意一点,∠ABD=∠ACE,BD=CE.
已知:点D是等边△ABC边上任意一点,∠ABD=∠ACE,BD=CE.