题目内容
 (2012•资阳)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接EP、CP、OP.
(2012•资阳)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连接DE,过点B作BP平行于DE,交⊙O于点P,连接EP、CP、OP.(1)BD=DC吗?说明理由;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线;
如果你解答这个问题有困难,可以参考如下信息:
为了解答这个问题,小明和小强做了认真的探究,然后分别用不同的思路完成了这个题目.在进行小组交流的时候,小明说:“设OP交AC于点G,证△AOG∽△CPG”;小强说:“过点C作CH⊥AB于点H,证四边形CHOP是矩形”.
分析:(1)连接AD,由圆周角定理可知∠ADB=90°,再由AB=AC可知△ABC是等腰三角形,故BD=DC;
(2)由于AD是等腰三角形ABC底边上的中线,所以∠BAD=∠CAD,故
=
,进而可得出BD=DE,故BD=DE=DC,
所以∠DEC=∠DCE,△ABC中由等腰三角形的性质可得出∠ABC=75°,故∠DEC=75°由三角形内角和定理得出∠EDC的度数,再根据BP∥DE可知∠PBC=∠EDC=30°,进而得出∠ABP的度数,再由OB=OP,可知∠OBP=∠OPB,由三角形内角和定理即可得出∠BOP=90°;
(3)设OP交AC于点G,由∠BOP=90°可知∠AOG=90°在Rt△AOG中,由∠OAG=30°,可知
=
,由于
=
=
,所以
=
,
=
,再根据∠AGO=∠CGP可得出△AOG∽△CPG,由相似三角形形的性质可知∠GPC=∠AOG=90°,故可得出CP是⊙O的切线.
(2)由于AD是等腰三角形ABC底边上的中线,所以∠BAD=∠CAD,故
 |
| BD |
 |
| DE |
所以∠DEC=∠DCE,△ABC中由等腰三角形的性质可得出∠ABC=75°,故∠DEC=75°由三角形内角和定理得出∠EDC的度数,再根据BP∥DE可知∠PBC=∠EDC=30°,进而得出∠ABP的度数,再由OB=OP,可知∠OBP=∠OPB,由三角形内角和定理即可得出∠BOP=90°;
(3)设OP交AC于点G,由∠BOP=90°可知∠AOG=90°在Rt△AOG中,由∠OAG=30°,可知
| OG |
| AG |
| 1 |
| 2 |
| OP |
| AC |
| OP |
| AB |
| 1 |
| 2 |
| OP |
| AC |
| OG |
| AG |
| OG |
| AG |
| GP |
| GC |
解答:(1)解:BD=DC.
连接AD,如图1,
∵AB是直径,
∴∠ADB=90°,
∵AB=AC,
∴BD=DC;
(2)解:∵AD是等腰三角形ABC底边上的中线,
∴∠BAD=∠CAD,
∴
=
,
∴BD=DE,
∴BD=DE=DC,
∴∠DEC=∠DCE,
∵△ABC中,AB=AC,∠A=30°
∴∠DCE=∠ABC=
(180°-30°)=75°,
∴∠DEC=75°
∴∠EDC=180°-75°-75°=30°
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠ABP=∠ABC-∠PBC=75°-30°=45°
∵OB=OP,
∴∠OBP=∠OPB=45°,
∴∠BOP=90°;

(3)证明:证法一:
∵设OP交AC于点G,则∠AOG=∠BOP=90°
∴OP⊥AB
在Rt△AOG中,
∵∠OAG=30°,
∴
=
,
又∵
=
=
,
∴
=
,
∴
=
,
又∵∠AGO=∠CGP
∴△AOG∽△CPG,
∴∠GPC=∠AOG=90°,
∴CP是⊙O的切线.
证法二:过点C作CH⊥AB于点H,如图2,则∠BOP=∠BHC=90°,
∴PO∥CH
在Rt△AHC中,
∵∠HAC=30°,
∴CH=
AC,
又∵PO=
AB=
AC,
∴PO=CH,
∴四边形CHOP是平行四边形
∵CH⊥AB,
∴四边形CHOP是矩形,
又∵点P在圆O上,
∴∠OPC=90°,即OP⊥PC,
∴CP是⊙O的切线.
连接AD,如图1,
∵AB是直径,
∴∠ADB=90°,
∵AB=AC,
∴BD=DC;
(2)解:∵AD是等腰三角形ABC底边上的中线,
∴∠BAD=∠CAD,
∴
 |
| BD |
 |
| DE |
∴BD=DE,
∴BD=DE=DC,
∴∠DEC=∠DCE,
∵△ABC中,AB=AC,∠A=30°
∴∠DCE=∠ABC=
| 1 |
| 2 |
∴∠DEC=75°
∴∠EDC=180°-75°-75°=30°
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠ABP=∠ABC-∠PBC=75°-30°=45°
∵OB=OP,
∴∠OBP=∠OPB=45°,
∴∠BOP=90°;

(3)证明:证法一:
∵设OP交AC于点G,则∠AOG=∠BOP=90°
∴OP⊥AB
在Rt△AOG中,
∵∠OAG=30°,
∴
| OG |
| AG |
| 1 |
| 2 |
又∵
| OP |
| AC |
| OP |
| AB |
| 1 |
| 2 |
∴
| OP |
| AC |
| OG |
| AG |
∴
| OG |
| AG |
| GP |
| GC |
又∵∠AGO=∠CGP
∴△AOG∽△CPG,
∴∠GPC=∠AOG=90°,
∴CP是⊙O的切线.
证法二:过点C作CH⊥AB于点H,如图2,则∠BOP=∠BHC=90°,
∴PO∥CH
在Rt△AHC中,
∵∠HAC=30°,
∴CH=
| 1 |
| 2 |
又∵PO=
| 1 |
| 2 |
| 1 |
| 2 |
∴PO=CH,
∴四边形CHOP是平行四边形
∵CH⊥AB,
∴四边形CHOP是矩形,
又∵点P在圆O上,
∴∠OPC=90°,即OP⊥PC,
∴CP是⊙O的切线.
点评:本题考查的是切线的判定定理、等腰三角形的性质、圆周角定理及相似三角形的判定与性质,在判定圆的切线时构造直角三角形,再利用直角三角形的性质去证明过圆心的直线与切线垂直.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 (2012•资阳)如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )
(2012•资阳)如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c<0的解集是( )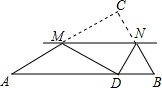 (2012•资阳)如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=
(2012•资阳)如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=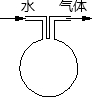 (2012•资阳)如图所示的球形容器上连接着两根导管,容器中盛满了不溶于水的比空气重的某种气体,现在要用向容器中注水的方法来排净里面的气体.水从左导管匀速地注入,气体从右导管排出,那么,容器内剩余气体的体积与注水时间的函数关系的大致图象是( )
(2012•资阳)如图所示的球形容器上连接着两根导管,容器中盛满了不溶于水的比空气重的某种气体,现在要用向容器中注水的方法来排净里面的气体.水从左导管匀速地注入,气体从右导管排出,那么,容器内剩余气体的体积与注水时间的函数关系的大致图象是( )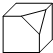 (2012•资阳)如图是一个正方体被截去一角后得到的几何体,它的俯视图是( )
(2012•资阳)如图是一个正方体被截去一角后得到的几何体,它的俯视图是( )