Question

【题目】如图，抛物线顶点为A（2，4），且过原点，与x轴的另一个交点为B，

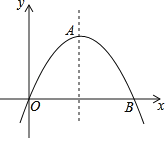
①求抛物线的解析式；

②求△AOB面积；

③抛物线上是否存在点M，使△OBM的面积等于10？若存在，求出M点坐标，若不存在，说明理由；

Answer 1

【答案】①y＝﹣（x﹣2）2+4或y＝﹣x2+4x；②8；③存在，理由见解析；

【解析】

①设顶点式为y＝a（x﹣2）2+4，然后把原点坐标代入求出a即可；

②通过解方程﹣x2+4x＝0得B（4，0），然后根据三角形面积公式计算；

③设M点坐标为（x，﹣x2+4x），由于△AOB面积为8，则可判断M点在x轴下方，利用三角形的面积公式得到×4×（x2﹣4x）]＝10，然后求出x即可得到M点的坐标．

解：①设抛物线解析式为y＝a（x﹣2）2+4，

把（0，0）代入得a（0﹣2）2+4＝0，解得a＝﹣1，

∴抛物线解析式为y＝﹣（x﹣2）2+4或y＝﹣x2+4x；

②解方程﹣x2+4x＝0得x1＝0，x2＝4，则B（4，0），

∴△AOB面积＝×4×4＝8；

③存在．

设M点坐标为（x，﹣x2+4x），

∵△AOB面积为8，

∴M点在x轴下方，

∴×4×（x2﹣4x）]＝10，

整理得x2﹣4x﹣5＝0，解得x1＝﹣1，x2＝5，

此时M点的坐标为（﹣1，﹣5），（5，﹣5）．