题目内容
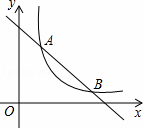
如图,在直角坐标系中,直线y=6﹣x与函数![]() (x>0)的图象相交于点A、B,设A点的坐标为(x1,y1),那么长为x1,宽为y1的矩形面积和周长分别是( )
(x>0)的图象相交于点A、B,设A点的坐标为(x1,y1),那么长为x1,宽为y1的矩形面积和周长分别是( )
|
| A. | 4,12 | B. | 4,6 | C. | 8,12 | D. | 8,6 |
考点:
反比例函数与一次函数的交点问题.
专题:
探究型.
分析:
先根据两函数图象的交点在第一象限可知x>0,y>0,再根据两函数有交点可列出关于x、y的方程组,求出x,y的值,再根据矩形的面积及周长公式进行解答即可.
解答:
解:∵两函数图象的交点在第一象限,
∴x>0,y>0,
∴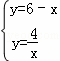 ,
,
∴![]() =6﹣x,
=6﹣x,
∴x2﹣6x+4=0,
解得x=3±![]() ,
,
∵A在B的左边,
∴x=3﹣![]() ,y=3+
,y=3+![]() ,即A(3﹣
,即A(3﹣![]() ,3+
,3+![]() ),
),
∴矩形的面积=(3﹣![]() )(3+
)(3+![]() )=4;
)=4;
矩形的周长=2(3﹣![]() )+2(3+
)+2(3+![]() )=12.
)=12.
故选A.
点评:
本题考查的是一次函数与反比例函数的交点问题,根据题意得出关于x、y的方程组是解答此题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: