题目内容
已知二次函数y=ax2图象上有两点A、B,横坐标分别为-2、1,若△ABO为直角三角形,求a的值.
【答案】分析:作出草图,过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,然后表示出AC、BD的长,再求出∠AOC=∠OBD,求出△AOC和△OBD相似,再根据相似三角形对应边成比例列式计算即可得解.
解答: 解:如图,过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
解:如图,过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
∵二次函数y=ax2图象上有两点A、B,横坐标分别为-2、1,
∴AC=4a,BD=a,
∵△ABO为直角三角形,
∴∠AOB=90°,
∴∠AOC+∠BOD=90°,
又∵∠OBD+∠BOD=90°,
∴∠AOC=∠OBD,
∴△AOC∽△OBD,
∴ =
= ,
,
即 =
= ,
,
解得a=± .
.
点评:本题考查了二次函数图象上点的坐标特征,主要利用了相似三角形的判定与性质,作出图形更形象直观.
解答:
 解:如图,过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
解:如图,过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,∵二次函数y=ax2图象上有两点A、B,横坐标分别为-2、1,
∴AC=4a,BD=a,
∵△ABO为直角三角形,
∴∠AOB=90°,
∴∠AOC+∠BOD=90°,
又∵∠OBD+∠BOD=90°,
∴∠AOC=∠OBD,
∴△AOC∽△OBD,
∴
 =
= ,
,即
 =
= ,
,解得a=±
 .
.点评:本题考查了二次函数图象上点的坐标特征,主要利用了相似三角形的判定与性质,作出图形更形象直观.

练习册系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
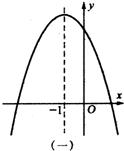 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
