题目内容
已知:函数y=-
x2+x+a的图象的最高点在x轴上.
(1)求a;
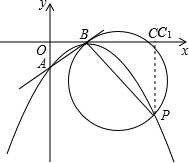
(2)如图所示,设二次函数y=-
x2+x+a图象与y轴的交点为A,顶点为B,P为图象上的一点,若以线段PB为直径的圆与直线AB相切于点B,求P点的坐标;
(3)在(2)中,若圆与x轴另一交点C关于直线PB的对称点为M,试探索点M是否在抛物线y=-
x2+x+a上?若在抛物线上,求出M点的坐标;若不在,请说明理由.

| 1 |
| 4 |
(1)求a;
(2)如图所示,设二次函数y=-
| 1 |
| 4 |
(3)在(2)中,若圆与x轴另一交点C关于直线PB的对称点为M,试探索点M是否在抛物线y=-
| 1 |
| 4 |

(1)依题意有△=1+a=0,
解得a=-1;
 (2)设P为二次函数图象上的一点,过点P作PC⊥x轴于点C1;
(2)设P为二次函数图象上的一点,过点P作PC⊥x轴于点C1;
∵y=-
x2+x-1顶点为B(-2,0),图象与y轴的交点坐标为A(0,-1),
∵以PB为直径的圆与直线AB相切于点B,
∴PB⊥AB,则∠PBC1=∠BAO
∴Rt△PC1B∽Rt△BOA
∴
=
,故PC1=2BC1,
设P点的坐标为(x,y),
∵∠ABO是锐角,∠PBA是直角,
∴∠PBO是钝角,
∴x>2
∴BC1=x-2,PC1=2x-4,
即y=4-2x,
∴P点的坐标为(x,4-2x)
∵点P在二次函数y=-
x2+x+1的图象上,
∴4-2x=-
x2+x-1,
解得:x1=-2,x2=10
∵x>2,
∴x=10,
∴P点的坐标为:(10,-16);
(3)点M不在抛物线y=-
x2+x+a上,
由(2)知:C1为圆与x轴的另一交点,连接CM,CM与直线PB的交点为Q,过点M作x轴的垂线,垂足为D,取CD的中点E,连接QE,则CM⊥PB,且CQ=MQ,
∴QE∥MD,QE=
MD,QE⊥CE
∵CM⊥PB,QE⊥CE,PC⊥x轴
∴∠QCE=∠EQB=∠CPB
∴tan∠QCE=tan∠EQB=tan∠CPB=
,
CE=2QE=2×2BE=4BE,
又∵CB=8,
故BE=
,QE=
,
∴Q点的坐标为(
,-
)
可求得M点的坐标为(
,-
)
∵-
×(
)2+
-1=-
≠-
,
∴C点关于直线PB的对称点M不在抛物线y=-
x2+x+a上.
解得a=-1;
 (2)设P为二次函数图象上的一点,过点P作PC⊥x轴于点C1;
(2)设P为二次函数图象上的一点,过点P作PC⊥x轴于点C1;∵y=-
| 1 |
| 4 |
∵以PB为直径的圆与直线AB相切于点B,
∴PB⊥AB,则∠PBC1=∠BAO
∴Rt△PC1B∽Rt△BOA
∴
| PC1 |
| OB |
| BC1 |
| AO |
设P点的坐标为(x,y),
∵∠ABO是锐角,∠PBA是直角,
∴∠PBO是钝角,
∴x>2
∴BC1=x-2,PC1=2x-4,
即y=4-2x,
∴P点的坐标为(x,4-2x)
∵点P在二次函数y=-
| 1 |
| 4 |
∴4-2x=-
| 1 |
| 4 |
解得:x1=-2,x2=10
∵x>2,
∴x=10,
∴P点的坐标为:(10,-16);
(3)点M不在抛物线y=-
| 1 |
| 4 |
由(2)知:C1为圆与x轴的另一交点,连接CM,CM与直线PB的交点为Q,过点M作x轴的垂线,垂足为D,取CD的中点E,连接QE,则CM⊥PB,且CQ=MQ,
∴QE∥MD,QE=
| 1 |
| 2 |
∵CM⊥PB,QE⊥CE,PC⊥x轴
∴∠QCE=∠EQB=∠CPB
∴tan∠QCE=tan∠EQB=tan∠CPB=
| 1 |
| 2 |
CE=2QE=2×2BE=4BE,
又∵CB=8,
故BE=
| 8 |
| 5 |
| 16 |
| 5 |
∴Q点的坐标为(
| 18 |
| 5 |
| 16 |
| 5 |
可求得M点的坐标为(
| 14 |
| 5 |
| 32 |
| 5 |
∵-
| 1 |
| 4 |
| 14 |
| 5 |
| 14 |
| 5 |
| 144 |
| 25 |
| 32 |
| 5 |
∴C点关于直线PB的对称点M不在抛物线y=-
| 1 |
| 4 |

练习册系列答案
相关题目




 PE与直线AB交于点E.
PE与直线AB交于点E.