Question

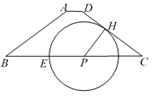
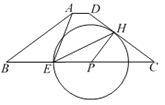
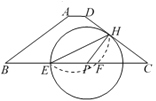
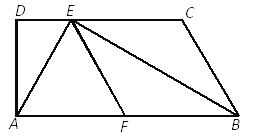
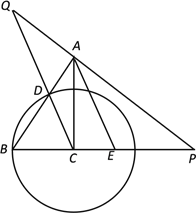
【题目】如图，已知Rt△ABC 中，∠ACB=90°，BC=2，AC=3，以点C为圆心、CB为半径的圆交AB于点D，过点A作AE∥CD，交BC延长线于点E.

（1）求CE的长；

（2）P是 CE延长线上一点，直线AP、CD交于点Q.

①如果△ACQ ∽△CPQ，求CP的长；

②如果以点A为圆心，AQ为半径的圆与⊙C相切，求CP的长.

Answer 1

【答案】（1）CE=；（2）①；②

【解析】分析：（1）由平行线分线段成比例定理得：．再由BC=DC，得到BE=AE．设CE=x，则AE=BE=x+2．在Rt△ACE中，由勾股定理即可得出结论．

（2）①由△ACQ ∽△CPQ，得到∠ACQ=∠P．再由平行线的性质得到∠ACQ=∠CAE，则∠CAE=∠P，即可证明△ACE ∽△PCA，由相似△的性质即可得到结论．

②设CP=t，则 ．在Rt△ACP中，由勾股定理得： ．

再由平行线分线段成比例定理得，可求出．然后分两种情况讨论：①若两圆外切，则，②若两圆内切，则，解方程即可．

详解：（1）∵AE∥CD，∴．∵BC=DC，∴BE=AE．

设CE=x，则AE=BE=x+2．

∵ ∠ACB=90°，∴ ，即，∴，即．

（2）①∵△ACQ ∽△CPQ，∠QAC>∠P，∴∠ACQ=∠P．

又∵AE∥CD，∴∠ACQ=∠CAE，∴∠CAE=∠P，

∴△ACE ∽△PCA，

∴，

即，

∴ ．

②设CP=t，则 ．

∵∠ACB=90°，∴ ．

∵AE∥CD，∴，即，∴．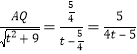

若两圆外切，那么，此时方程无实数解．

若两圆内切，那么，∴ ，解得．

又∵，∴．